Interpreting convex integration results in hydrodynamics

1 Introduction

Convex integration techniques, introduced in the context of differential geometry by Nash [⁠39⁠ J. Nash, C1 isometric imbeddings. Ann. of Math. (2) 60, 383–396 (1954) ] and Gromov [⁠27⁠ M. L. Gromov, Convex integration of differential relations. I. Izv. Akad. Nauk SSSR Ser. Mat. 37, 329–343 (1973) ], have been later applied to fluid dynamics by De Lellis and Székelyhidi in the path-breaking papers [⁠14⁠ C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009) , ⁠15⁠ C. De Lellis and L. Székelyhidi, Jr., On admissibility criteria for weak solutions of the Euler equations. Arch. Ration. Mech. Anal. 195, 225–260 (2010) ]. Subsequently, these techniques have been used with great success by many researchers to prove inter alia non-uniqueness of weak solutions of Euler and Navier–Stokes equations. A recent review of the technique is provided in the monograph by Markfelder [⁠37⁠ S. Markfelder, Convex integration applied to the multi-dimensional compressible Euler equations. Lecture Notes in Math. 2294, Springer, Cham (2021) ]. Below we refer to weak solutions obtained by convex integration techniques as wild solutions.

The question of present concern is what relevance these outstanding mathematical results have for the prediction and explanation of observed physical phenomena. For definiteness, consider the striking result proved by Buckmaster and Vicol [⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) ]:

A remarkable feature of this result is that the function $e(\cdot )$ does not have to be decreasing in time. The Buckmaster–Vicol theorem implies non-uniqueness of weak solutions of the Navier–Stokes equations on the 3-torus ${\mathbb{T}}^3$ as $e(\cdot )$ can have compact support. These wild velocity fields exhibit a strong degree of irregularity.

Although this theorem is clearly a great achievement of 21st century analysis, its relevance to turbulence and other observed fluid behaviour is not obvious and indeed is disputed by some. It is a potentially rich topic for discussion.

Thus, with the aim of making available to the wider scientific community differing views on this important subject, we⁠¹⁠Here and in Section ⁠3⁠ “we” means H. Gimperlein, M. Grinfeld, R. J. Knops and M. Slemrod. approached for their opinion a representative cross-section of leading practitioners not only in mathematics and physics, but also in philosophy of physics and mathematics.

Accordingly, we invited answers to the following specific question:

How, in your opinion, does the theorem of Buckmaster and Vicol relate to the prediction of observed fluid flows?

Section ⁠2⁠ contains the replies we have received. Section ⁠3⁠ summarises the discussion and contributes some concluding remarks.

To give the reader some guidance, we now describe how the contributors see their scientific outlook. Gregory Eyink and Nigel Goldenfeld are theoretical physicists with a wide range of interests, who, to quote Eyink, try “to talk with everyone and understand everyone, including philosophers, mathematicians, physicists, chemists, engineers, etc.”; Ondřej Kreml is primarily a mathematician with a background in physics and mathematical modelling; Ilya Karlin and Florian Kogelbauer are applied mathematicians and mathematical physicists; Colin McLarty is a philosopher and a mathematician; Simon Markfelder defines himself as a mathematician, Mikhail Osipov is a theoretical physicist and an applied mathematician. We (understood in the sense of footnote 1) see ourselves as mathematicians who worry about the connections of mathematics with the natural world.

2 Expert opinions

This section reproduces in full the replies received to our invitation.

2.1 Gregory Eyink and Nigel Goldenfeld

The question posed is whether there is any physical relevance of the convex integration techniques of Nash and Gromov, as successfully applied by De Lellis and Székelyhidi [⁠14⁠ C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009) , ⁠15⁠ C. De Lellis and L. Székelyhidi, Jr., On admissibility criteria for weak solutions of the Euler equations. Arch. Ration. Mech. Anal. 195, 225–260 (2010) ] to the mathematics of the partial differential equations of continuum fluid mechanics. A particular focus is the remarkable result of Buckmaster and Vicol [⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) ] proving non-uniqueness of incompressible Navier–Stokes solutions for fixed initial data. In fact, they proved the existence of weak Navier–Stokes solutions whose kinetic energy is any prescribed non-negative function. Here, as requested, we point out what aspects of this body of work are likely to be physically relevant to hydrodynamics, and which are of purely mathematical interest. We focus on turbulence in particular. Our conclusion is that the potentially important application of convex integration to hydrodynamic turbulence is to show the non-uniqueness of solutions of the Euler equations, not the Navier–Stokes equations! The reason is that it is the Euler solutions which describe the inertial-range cascade at asymptotically large Reynolds numbers [⁠40⁠ L. Onsager, Statistical hydrodynamics. Nuovo Cimento (9) 6, 279–287 (1949) ], and the convex integration proofs of their non-uniqueness establish a prerequisite for the conjectured phenomenon of spontaneous stochasticity induced by thermal fluctuations [⁠4⁠ D. Bandak, A. A. Mailybaev, G. L. Eyink and N. Goldenfeld, Spontaneous stochasticity amplifies even thermal noise to the largest scales of turbulence in a few eddy turnover times. Phys. Rev. Lett. 132, article no. 104002 (2024) , ⁠21⁠ G. L. Eyink and L. Peng, Space-time statistical solutions of the incompressible Euler equations and Landau–Lifshitz fluctuating hydrodynamics. arXiv:2409.13103v1 (2024) ].

As physicists, our perspective is based on the physical relevance and structural stability of the starting assumptions, specifically the deterministic incompressible Navier–Stokes equations. These equations have been traditionally assumed in the fluid mechanics community to be valid at all scales down to the mean free path, where hydrodynamics must break down. However, molecular noise is required by the assumption of local thermal equilibrium and such noise produces many experimental effects in laminar flows that are missed by the deterministic equations [⁠50⁠ J. M. O. de Zárate and J. V. Sengers, Hydrodynamic fluctuations in fluids and fluid mixtures. Elsevier, Amsterdam (2006) ]. It was realised already by Landau and Lifschitz [⁠34⁠ L. D. Landau and E. M. Lifshitz, Fluid mechanics. Course of Theoretical Physics, Vol 6, Pergamon Press, London–Paris–Frankfurt; Addison-Wesley Publishing, Reading, MA (1959) ] that hydrodynamic equations need to incorporate thermal fluctuations together with viscous dissipation, and they formulated a successful theory of “fluctuating hydrodynamics” consistent with the fluctuation-dissipation theorem of statistical physics. Using a shell model of these equations, we recently showed, in a high-Reynolds turbulent flow at parameters relevant to the atmospheric boundary layer, that thermal fluctuations become significant already at the Kolmogorov scale, orders of magnitude larger than the mean free path length [⁠3⁠ D. Bandak, N. Goldenfeld, A. A. Mailybaev and G. Eyink, Dissipation-range fluid turbulence and thermal noise. Phys. Rev. E 105, article no. 065113 (2022) ]. Our result was subsequently confirmed by a numerical simulation at much lower Reynolds numbers, corresponding to a gently stirred vial of water, using the full Landau–Lifschitz equations [⁠7⁠ J. B. Bell, A. Nonaka, A. L. Garcia and G. Eyink, Thermal fluctuations in the dissipation range of homogeneous isotropic turbulence. J. Fluid Mech. 939, article no. A12 (2022) ]. Thus, we doubt the physical importance of the non-uniqueness results of Buckmaster and Vicol [⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) ] because the deterministic Navier–Stokes equations which they study are based on an unphysical continuum approximation. The Landau–Lifschitz equations, on the contrary, are easily proved to have strong, pathwise-unique solutions (e.g., see [⁠1⁠ F. Flandoli, An introduction to 3d stochastic fluid dynamics. In SPDE in hydrodynamic: recent progress and prospects. Lecture Notes in Math. 1942, pp. 51–150, Springer, Berlin; Fondazione C.I.M.E., Florence (2008) ]), because they are understood to be a mesoscopic effective field theory with an explicit high-wavenumber cutoff.

Our claims may appear in contradiction with rigorous mathematical derivations of incompressible Navier–Stokes as a deterministic PDE by means of a hydrodynamic scaling limit, e.g., in stochastic lattice gas models [⁠41⁠ J. Quastel and H.-T. Yau, Lattice gases, large deviations, and the incompressible Navier–Stokes equations. Ann. of Math. (2) 148, 51–108 (1998) ]. These rigorous results support the so-called “macroscopic fluctuation theory” [⁠8⁠ L. Bertini, A. De Sole, D. Gabrielli, G. Jona-Lasinio and C. Landim, Macroscopic fluctuation theory. Rev. Modern Phys. 87, 593–636 (2015) ], according to which velocity fields evolve by deterministic Navier–Stokes, with probability going to one. This theory attempts to incorporate thermal fluctuations by probabilistic large deviations theory, in which spontaneous fluctuations arise in thermal equilibrium by “instanton solutions” governed by time-reversed Navier–Stokes equations with negative viscosity [⁠8⁠ L. Bertini, A. De Sole, D. Gabrielli, G. Jona-Lasinio and C. Landim, Macroscopic fluctuation theory. Rev. Modern Phys. 87, 593–636 (2015) ]. In that setting, the Buckmaster and Vicol wild solutions might be accorded physical significance, because, under time reversal, they could describe a very rare fluctuation in which the fluid spontaneously cools down and the lost thermal energy is converted into macroscopic kinetic energy. The Buckmaster–Vicol theorem suggests that such macroscopic thermal fluctuations could arise in a strictly finite time from the rest state of the fluid and likewise could decay back to rest in a finite time, whereas smooth Navier–Stokes solutions require infinite time [⁠43⁠ J. Serrin, The initial value problem for the Navier–Stokes equations. In Nonlinear Problems (Proc. Sympos., Madison, Wis., 1962), Univ. Wisconsin Press, Madison, WI, 69–98 (1963) ]. See Gess et al. [⁠24⁠ B. Gess, D. Heydecker and Z. Wu, Landau–Lifshitz–Navier–Stokes equations: Large deviations and relationship to the energy equality. arXiv:2311.02223v2 ([v1] 2023, [v2] 2024) ] for a recent discussion of the Buckmaster–Vicol theorem in the context of macroscopic fluctuation theory. However, this interpretation of the Buckmaster–Vicol theorem is also unphysical in our opinion, because the “hydrodynamic scaling limit” invoked in macroscopic fluctuation theory is essentially impossible to achieve in any realistic molecular fluid. Indeed, the numerical counterexamples of Bandak et al. [⁠3⁠ D. Bandak, N. Goldenfeld, A. A. Mailybaev and G. Eyink, Dissipation-range fluid turbulence and thermal noise. Phys. Rev. E 105, article no. 065113 (2022) ] and Bell et al. [⁠7⁠ J. B. Bell, A. Nonaka, A. L. Garcia and G. Eyink, Thermal fluctuations in the dissipation range of homogeneous isotropic turbulence. J. Fluid Mech. 939, article no. A12 (2022) ] showed that the thermal fluctuation effects can never be removed in practice even if the flow were scaled by ridiculously large factors of millions or billions!

In our opinion, convex integration techniques have physical relevance for turbulent fluids not when applied to Navier–Stokes but instead to Euler equations. Unlike the Navier–Stokes equations, the inviscid Euler equations have a precise physical regime of validity, since their weak solutions plausibly describe the inertial range of turbulent flows at very high Reynolds numbers ([⁠40⁠ L. Onsager, Statistical hydrodynamics. Nuovo Cimento (9) 6, 279–287 (1949) ]; for a detailed review, see [⁠20⁠ G. Eyink, Onsager’s ‘ideal turbulence’ theory. J. Fluid Mech. 988, article no. P1 (2024) ]). The inertial range is described by continuum PDEs not because the size of the smallest turbulent eddies shrinks below the molecular scale, but instead because the Kolmogorov length is much smaller than the outer scale of energy injection in the limit of large Reynolds numbers. Of particular physical significance are the convex integration proofs of non-uniqueness of weak solutions of the incompressible Euler equations with fixed initial data, even after imposing reasonable admissibility conditions such as dissipation of kinetic energy [⁠12⁠ S. Daneri, E. Runa and L. Székelyhidi, Non-uniqueness for the Euler equations up to Onsager’s critical exponent. Ann. PDE 7, article no. 8 (2021) , ⁠13⁠ C. De Lellis and H. Kwon, On nonuniqueness of Hölder continuous globally dissipative Euler flows. Anal. PDE 15, 2003–2059 (2022) ]. The non-uniqueness of the Euler solutions suggests an intrinsic unpredictability or “spontaneous stochasticity” of turbulent flow at high enough Reynolds number. In fact, in recent work we have provided strong numerical evidence in the context of a shell model of the turbulent cascade that such stochastic behaviour with fixed deterministic initial data may be triggered by vanishingly small thermal noise [⁠4⁠ D. Bandak, A. A. Mailybaev, G. L. Eyink and N. Goldenfeld, Spontaneous stochasticity amplifies even thermal noise to the largest scales of turbulence in a few eddy turnover times. Phys. Rev. Lett. 132, article no. 104002 (2024) ]. Furthermore, we have proved using the physical Landau–Lifschitz equations that such persistent stochasticity requires non-uniqueness of the Euler solutions [⁠21⁠ G. L. Eyink and L. Peng, Space-time statistical solutions of the incompressible Euler equations and Landau–Lifshitz fluctuating hydrodynamics. arXiv:2409.13103v1 (2024) ], exactly the condition established by the breakthrough methods of convex integration theory.

2.2 Ilya Karlin and Florian Kogelbauer

Convex integration is a powerful mathematical tool that allows for the construction of exotic solutions to partial differential equations – solutions that defy classical intuition and exist even when standard methods fail or when uniqueness is lost [⁠11⁠ T. Buckmaster and V. Vicol, Convex integration constructions in hydrodynamics. Bull. Amer. Math. Soc. (N.S.) 58, 1–44 (2021) ]. Originally introduced by Nash in the study of isometric embeddings [⁠39⁠ J. Nash, C1 isometric imbeddings. Ann. of Math. (2) 60, 383–396 (1954) ], the technique was later expanded by Gromov and Eliashberg [⁠27⁠ M. L. Gromov, Convex integration of differential relations. I. Izv. Akad. Nauk SSSR Ser. Mat. 37, 329–343 (1973) ] in the realm of geometric PDEs.

Its impact on fluid dynamics became evident with the groundbreaking work of De Lellis and Székelyhidi [⁠14⁠ C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009) , ⁠15⁠ C. De Lellis and L. Székelyhidi, Jr., On admissibility criteria for weak solutions of the Euler equations. Arch. Ration. Mech. Anal. 195, 225–260 (2010) ], who applied convex integration to construct weak solutions of the unforced Euler equations. Building on their insights, Buckmaster and Vicol revealed something striking: the existence of weak solutions to the unforced Navier–Stokes equations with arbitrary energy growth, as described in Theorem ⁠1.1⁠ above.

The existence of wild solutions ties deeply into the phenomenon of anomalous dissipation in turbulence. Onsager’s famous conjecture states that weak solutions of the Euler equations with regularity above the critical $C^{1/3}$ threshold conserve energy, while rougher solutions may dissipate it anomalously [⁠40⁠ L. Onsager, Statistical hydrodynamics. Nuovo Cimento (9) 6, 279–287 (1949) ]. Could a similar Onsager-type condition emerge for the Navier–Stokes equations, delineating when turbulent energy cascades lead to dissipation [⁠18⁠ J. Duchon and R. Robert, Inertial energy dissipation for weak solutions of incompressible Euler and Navier–Stokes equations. Nonlinearity 13, 249–255 (2000) ]? Despite their mathematical validity, wild solutions pose another important question: Are they physically observable? Can their bizarre behaviour – such as unbounded kinetic energy growth – be reproduced in a real-world experiment? Or is there some physical obstruction that prevents their manifestation in nature?

It seems that the puzzling properties of wild solutions, especially the loss of uniqueness, are contradictory to physically observable fluid flows and thus require further restrictions on the fluid initial conditions, i.e., a selection criterion similar to stability for dynamically observable states [⁠46⁠ L. M. Silverman and B. D. O. Anderson, Controllability, observability and stability of linear systems. SIAM J. Control 6, 121–130 (1968) ]. A recent variational admissibility principle proposed for the Euler equations [⁠25⁠ H. Gimperlein, M. Grinfeld, R. J. Knops and M. Slemrod, The least action admissibility principle. Arch. Ration. Mech. Anal. 249, article no. 22 (2025) ] may serve as a step toward addressing this issue in the Navier–Stokes setting as well.

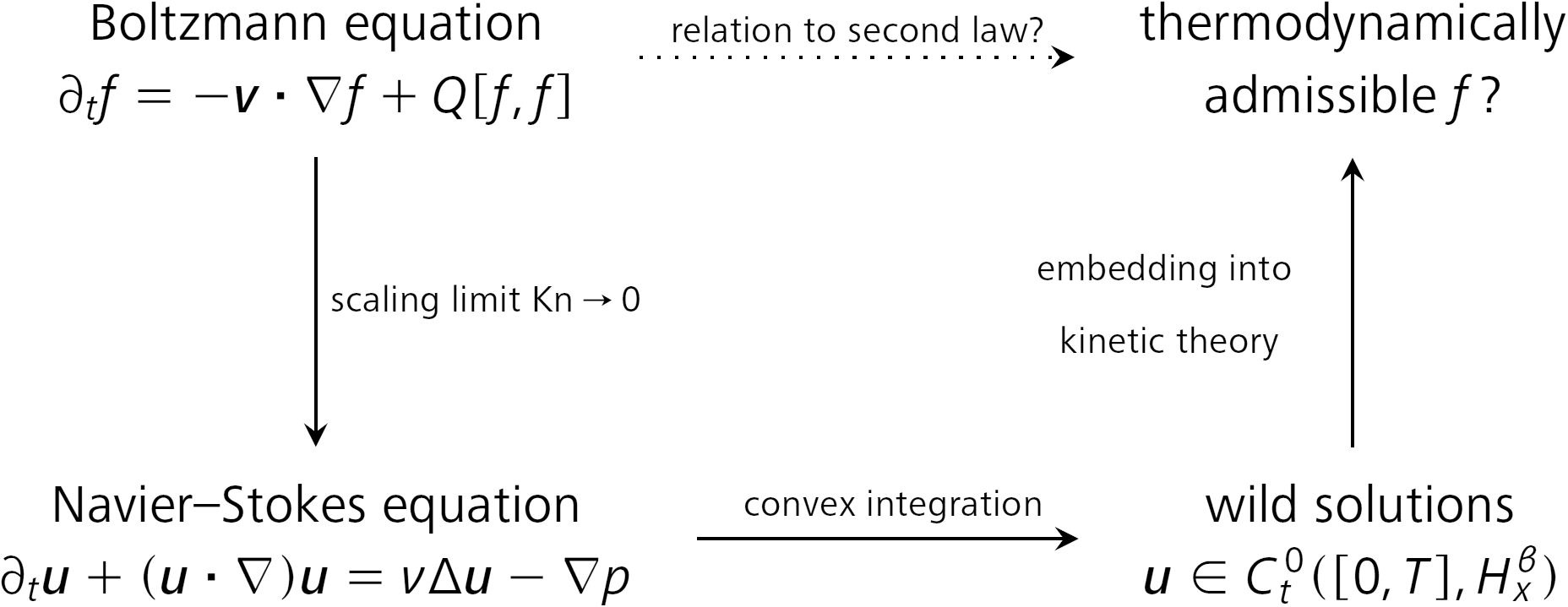
From a broader perspective, the Navier–Stokes equations arise as a scaling limit of the Boltzmann equation in the regime of vanishing Knudsen number – the ratio of the mean free path to a system’s characteristic length scale [⁠5⁠ C. Bardos, F. Golse and C. D. Levermore, Fluid dynamic limits of kinetic equations. II. Convergence proofs for the Boltzmann equation. Comm. Pure Appl. Math. 46, 667–753 (1993) , ⁠26⁠ F. Golse and L. Saint-Raymond, The Navier–Stokes limit of the Boltzmann equation for bounded collision kernels. Invent. Math. 155, 81–161 (2004) , ⁠35⁠ P.-L. Lions and N. Masmoudi, From the Boltzmann equations to the equations of incompressible fluid mechanics. I. Arch. Ration. Mech. Anal. 158, 173–193 (2001) , ⁠36⁠ P.-L. Lions and N. Masmoudi, From the Boltzmann equations to the equations of incompressible fluid mechanics. II. Arch. Ration. Mech. Anal. 158, 195–211 (2001) ]. At the kinetic level, entropy translates into kinetic energy at the fluid scale, meaning that unrestricted energy growth in the Navier–Stokes framework would be in conflict with the second law of thermodynamics [⁠47⁠ C. Truesdell and R. G. Muncaster, Fundamentals of Maxwell’s kinetic theory of a simple monatomic gas: Treated as a branch of rational mechanics. Pure Appl. Math. 83, Academic Press, Harcourt Brace Jovanovich, Publishers, New York–London (1980) ].

The previously raised question can thus be reformulated as: How do wild solutions of the Navier–Stokes equations relate to solutions of the Boltzmann equation? We know from the iterative structure of convex integration that these solutions involve extreme oscillations at very fine spatial scales [⁠11⁠ T. Buckmaster and V. Vicol, Convex integration constructions in hydrodynamics. Bull. Amer. Math. Soc. (N.S.) 58, 1–44 (2021) ]. However, at any finite Knudsen number, the hydrodynamic description is constrained by a critical wave number beyond which the Navier–Stokes model may break down [⁠32⁠ F. Kogelbauer and I. Karlin, Rigorous hydrodynamics from linear Boltzmann equations and viscosity-capillarity balance. Phys. Rev. E 110, article no. 055105 (2024) ].

Building on these insights, we propose the following conjecture: There exists a critical Onsager-type regularity threshold for Navier–Stokes solutions beyond which anomalous dissipation is no longer possible. Moreover, wild solutions of the Navier–Stokes equations cannot be derived from thermodynamically admissible kinetic states within the Boltzmann framework. In other words, the extreme irregularity and energy growth of these solutions may be fundamentally incompatible with the underlying kinetic theory governing physically observable fluids.

2.3 Ondřej Kreml

Recent convex integration results in the analysis of systems of partial differential equations describing fluid flows remind us that the equations we work with are merely simplified models of reality, and scientists should treat them as such. These models are highly useful in some scenarios, while in others, they may simply be unsuitable. This is evident in the case of the Euler equations, as physical fluids always have some nonzero viscosity, but to a certain extent, it also applies to the Navier–Stokes system.

Theorems stating the existence of infinitely many solutions to systems of equations used as models of reality suggest that the very definition of a solution may need careful reconsideration. It is well known that in the case of hyperbolic conservation laws, merely satisfying the weak formulation of the equations is insufficient to single out a unique solution. Additional admissibility criteria must be considered to determine what can be regarded as a physically meaningful solution. For the compressible Euler system in multiple space dimensions, identifying the correct notion of a solution that possesses the desired properties remains an open problem.

It may well be that, similar to hyperbolic conservation laws, the theorem by Buckmaster and Vicol for the Navier–Stokes equations establishes the existence of solutions that are not physically relevant. Only one – or perhaps none – of these solutions may accurately describe the behaviour of real fluids. While the theorem is a fascinating mathematical result with significant implications for the analysis of PDEs, its most important contribution to predicting real fluid behaviour may lie in reminding us that further work may be needed to identify the correct notion of a physical solution for some models describing physical processes.

2.4 Colin McLarty

It is an understatement to say convex integration gives beautifully motivated proofs of surprising geometric results. Beyond surprising, these results have been called “wild,” and “paradoxical,” and a Quanta magazine headline says they mark “where shapes give way” [⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) , ⁠42⁠ M. Rorvig, Mathematicians identify threshold at which shapes give way. (2021) https://www.quantamagazine.org/mathematicians-identify-threshold-at-which-shapes-give-way-20210603, ⁠48⁠ C. Villani, Paradoxe de Scheffer–Shnirelman revu sous l’angle de l’intégration convexe (d’après C. De Lellis et L. Székelyhidi). Astérisque 332, article no. 1001 (2010) ]. So the question arises: have these results any physical relevance? In particular, De Lellis and Székelyhidi [⁠14⁠ C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009) ], and then Buckmaster and Vicol [⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) ], use convex integration for striking, mathematically revealing, physically shocking solutions to the Euler and Navier–Stokes equations. A fluid completely stationary for some time, and subject to no external force, suddenly bursts into rapid motion, and after some time moving with however high kinetic energy you choose, it returns to complete rest. No one expects to see this in real fluids. Does that make the results irrelevant to real fluid dynamics?

History and philosophy of science have developed terms for discussing this kind of novelty, as for example in Thomas Kuhn’s Structure of Scientific Revolutions [⁠33⁠ T. S. Kuhn, The structure of scientific revolutions. University of Chicago Press, Chicago (1962) ]. This book is not all about revolutions. To the contrary, Kuhn says a successful science normally has a widely accepted theory, together with recognized means of interpreting that theory in observational data, and specific research problems, accepted research methods, and landmark successes. He calls the bundle of a theory, problems, methods, and exemplary achievements a paradigm.⁠²⁠Kuhn refined his terminology in later editions, but we can use the original. A productive science normally faces some empirical problems applying the theory to observed facts, and also conceptual difficulties extending the theory and saying exactly how the theoretical terms are meant to connect with observations. Kuhn [⁠33⁠ T. S. Kuhn, The structure of scientific revolutions. University of Chicago Press, Chicago (1962) , Chapter IV] compares these problems to puzzles in this sense: Facing a new crossword or jigsaw puzzle you cannot immediately solve it, but you assume it has a solution of known form, which can be found by skilful use of the known rules. Most often in a successful science that is what happens. Every once in a while a problem, which might not even seem like a big problem at first, grows in prominence to a point where practitioners feel it cannot be ignored, yet neither can it be settled by any of the standard means. It becomes a crisis and may eventuate in a revolution where the previously normal theory, methods, and questions give way to fundamentally new ones.

For our purposes the theory of fluid motion would be the Euler and Navier–Stokes equations [⁠23⁠ G. P. Galdi, An introduction to the mathematical theory of the Navier–Stokes equations: Steady-state problems. Second ed., Springer Monogr. Math., Springer, New York (2011) , p. 3]:

Till a few decades ago (early 1930s), there was unanimous opinion that the Navier–Stokes equations were useful (in agreement with the experiments, that is) only at “low” velocity regimes. It is also thanks to the efforts of outstanding mathematicians such as Jean Leray, Eberhard Hopf, Olga Ladyzhenskaya, and Robert Finn that they are nowadays regarded as the universal foundation of fluid mechanics.

In the vast literature on this theory the top questions are: Do the equations have smooth global solutions? Can this framework model turbulence? Convex integration points away from smoothness, but bears directly on turbulence [⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) , ⁠14⁠ C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009) , ⁠42⁠ M. Rorvig, Mathematicians identify threshold at which shapes give way. (2021) https://www.quantamagazine.org/mathematicians-identify-threshold-at-which-shapes-give-way-20210603, ⁠44⁠ A. Shnirelman, On the non-uniqueness of weak solution of the Euler equations. In Journées équations aux dérivées partielles, article no. 18 (1996) , ⁠48⁠ C. Villani, Paradoxe de Scheffer–Shnirelman revu sous l’angle de l’intégration convexe (d’après C. De Lellis et L. Székelyhidi). Astérisque 332, article no. 1001 (2010) ].

The theory is not the whole paradigm. The Euler and Navier–Stokes equations per se do not specify what kind of functions count as physically meaningful (weak) solutions [⁠38⁠ C. McLarty, Fluid mechanics for philosophers, or which solutions do you want for Navier–Stokes? In Working toward solutions in fluid dynamics and astrophysics: What the equations don’t say, SpringerBriefs Hist. Sci. Technol., Springer, Cham, 31–56 (2023) ]. This is wide open today. Restricting to smooth functions is too narrow for applications. Taking all Schwartz distributions is too broad. Moderately rough functions produce the paradoxical flows.

Villani notes the most direct way to rule out these paradoxical solutions to the Euler equation would be to explicitly require kinetic energy be conserved. Or more likely just require it not to increase, since a long tradition suggests turbulence dissipates kinetic energy. This is related to requiring solutions to be at least moderately smooth. Villani discusses the problems at length [⁠48⁠ C. Villani, Paradoxe de Scheffer–Shnirelman revu sous l’angle de l’intégration convexe (d’après C. De Lellis et L. Székelyhidi). Astérisque 332, article no. 1001 (2010) , pp. 105, 127f., 130]. These have got sharper with the recent work on Navier–Stokes, where viscosity also dissipates energy [⁠6⁠ J. Bedrossian and V. Vicol, The mathematical analysis of the incompressible Euler and Navier–Stokes equations: an introduction. Grad. Stud. Math. 225, American Mathematical Society, Providence, RI (2022) , ⁠10⁠ T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019) ].

Shnirelman offers an opposite approach: Instead of requiring moderately smooth solutions, allow even rougher initial conditions than Schwartz distributions. He suggests finer analytic tools (e.g., Young measures) might make the known paradoxical solutions less paradoxical, by revealing the fluid in them is not really at rest initially, but is just so “infinitely-fast oscillating in space” that even Schwartz distributions cannot resolve the motion [⁠44⁠ A. Shnirelman, On the non-uniqueness of weak solution of the Euler equations. In Journées équations aux dérivées partielles, article no. 18 (1996) , p. 3].

From our Kuhnian point of view, then, yes, the paradoxical uses of convex integration are an integral part of current fluid dynamics. They are at least a puzzle. A given researcher in either pure theory or applications might not be interested in the wild solutions—if they do not need any theory of turbulence. But the decisive points are: First, we have so far no articulable paradigm for fluid mechanics doing justice to current applications while either ruling out the paradoxical ones or clearing them of the air of paradox. And second, the paradoxical solutions fit within the current paradigm in the sense that they are publicly discussed by the normal means in the subject. This note will not speculate on whether this puzzle could one day grow to a crisis requiring a revolution in fluid dynamics.

2.5 Simon Markfelder

The question of the physical relevance of the theorem by Buckmaster–Vicol is strongly related to the question what is the right solution concept for the PDEs of mathematical fluid mechanics. The same holds for all the other results achieved by convex integration in the context of fluid dynamics.

Since the equations are supposed to model the real world (i.e., they should describe and predict what happens in nature), one at least expects existence and uniqueness of solutions. For the 2-D incompressible Euler and Navier–Stokes equations, strong solutions (i.e., solutions which are sufficiently differentiable) exist globally in time. Consequently, one may regard strong solutions as a good solution concept in this case. However, for the compressible Euler and Navier–Stokes equations, as well as the 3-D incompressible Euler equations, strong solutions only exist for small times and may blow up afterwards, see e.g., [⁠45⁠ T. C. Sideris, Formation of singularities in three-dimensional compressible fluids. Comm. Math. Phys. 101, 475–485 (1985) ], [⁠49⁠ Z. Xin, Blowup of smooth solutions to the compressible Navier–Stokes equation with compact density. Comm. Pure Appl. Math. 51, 229–240 (1998) ] and [⁠19⁠ T. Elgindi, Finite-time singularity formation for C1,α solutions to the incompressible Euler equations on \mathbb⁢R3. Ann. of Math. (2) 194, 647–727 (2021) ], respectively. Thus, in these cases the study of weak solutions (or even weaker solution concepts, see below) is unavoidable. Note, that for the 3-D incompressible Navier–Stokes equations whether smooth solutions exist globally in time or smooth solutions may blow up in finite time is an outstanding open question and is one of the famous millennium prize problems.

When considering weak solutions, an energy or entropy inequality has to be imposed in order to rule out unphysical solutions. This is a well-known fact in the context of systems of hyperbolic conservation laws like the compressible Euler equations. Moreover, energy/entropy inequalities can be justified from physics by thermodynamical explanations. Interestingly, both for the incompressible and the compressible Euler equations, the resulting concept of an admissible weak solution (i.e., a weak solution which complies with the corresponding energy/entropy inequality) does not lead to a unique solution, as shown by convex integration, see e.g., [⁠14⁠ C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009) , ⁠15⁠ C. De Lellis and L. Székelyhidi, Jr., On admissibility criteria for weak solutions of the Euler equations. Arch. Ration. Mech. Anal. 195, 225–260 (2010) ]. The result by Buckmaster and Vicol on the incompressible Navier–Stokes equations is of similar type, with the difference that their solutions do not satisfy the usual energy inequality (i.e., they are not Leray–Hopf weak solutions). This is due to the fact, that in the context of the Navier–Stokes equations, one needs some minimal regularity in order to make sense of the energy inequality, as it involves terms on the gradient of the solution. And the solutions obtained by Buckmaster and Vicol do not have this minimal regularity. Still they comply with any prescribed energy profile.

So, strictly speaking, there is still hope that the non-uniqueness issue raised by the Buckmaster–Vicol theorem does not have great relevance. Namely, if it turns out that strong solutions exist globally in time, then one may question the importance of weak solutions. Moreover, Leray–Hopf solutions might still be unique. And in this case, one may argue that the solutions obtained by Buckmaster and Vicol are just too weak, and thus irrelevant. On the other hand, in view of the aforementioned results, one should better not bet on either of the two possibilities. In addition to that, for the Euler equations we know already that neither the consideration of strong solutions, nor the study of admissible weak solutions leads to existence and uniqueness. So in my opinion, one has to discard the classical notion of admissible weak solutions, and look for novel solution concepts instead. I will discuss some of them in the sequel.

In the context of the Euler equations, people have studied additional criteria with the goal to select one among the infinitely many admissible weak solutions, e.g., one has considered the solution whose energy dissipation is maximal. So far, such additional criteria have however not led to a satisfactory solution concept. What people find quite promising in this direction, is the vanishing viscosity method. This would however require well-posedness for the corresponding viscous model, e.g., the Navier–Stokes equations. Another problem is that sequences of approximate solutions (like vanishing-viscosity sequences) usually exhibit oscillations and concentrations. Thus, the sequences in general only converge with respect to weak topologies. Moreover, by understanding the (weak) limit as a conventional function, one forgets the oscillatory and concentrative behaviour of the corresponding approximate sequence. A nice way to capture oscillations and concentration is to understand the limit as a (generalised) Young measure, which yields a probability distribution at each point in space-time instead of a particular value. This leads to the notion of a measure-valued solution, see e.g., [⁠2⁠ J. J. Alibert and G. Bouchitté, Non-uniform integrability and generalized Young measures. J. Convex Anal. 4, 129–147 (1997) , ⁠17⁠ R. J. DiPerna, Measure-valued solutions to conservation laws. Arch. Rational Mech. Anal. 88, 223–270 (1985) ]. It is in many situations not difficult to prove that approximate sequences converge to measure-valued solutions, which yields existence of the latter. This is in contrast to admissible weak solutions, which are—at least for the Euler equations—not known to exist. Moreover, the generalisation of weak solutions to measure-valued solutions also seems more plausible when turbulent flows are considered, since the statements of turbulence theory are of statistical nature.

However, the consideration of measure-valued instead of weak solutions does not solve the non-uniqueness problem. Quite the contrary is true, namely there are even more measure-valued solutions than weak solutions. For this reason, one has tried to impose selection criteria similar to the ones mentioned above in the context weak solutions, in order to identify the relevant solutions among the possibly many measure-valued solutions, see e.g., [⁠9⁠ D. Breit, E. Feireisl and M. Hofmanová, Solution semiflow to the isentropic Euler system. Arch. Ration. Mech. Anal. 235, 167–194 (2020) , ⁠22⁠ E. Feireisl, A. Jüngel and M. Lukáčová-Medvid’ová, Maximal dissipation and well-posedness of the Euler system of gas dynamics. arXiv:2501.05134v2 (2025) ]. Even though a satisfactory selection criterion has not been found yet, I feel that this approach is the most promising in order to find a good solution concept.

2.6 Mikhail Osipov

From the theoretical physics point of view, the theorem of Buckmaster and Vicol does not take into consideration that the Navier–Stokes equations are not a law of nature, but are approximate equations which are derived from the more general framework of molecular-statistical theory (e.g., from the BBGY chain of equations) using some important assumptions. In particular, these equations (as all classical hydrodynamics) are formally derived in the limit $k\to 0$, where $k$ is the wave number. More subtle assumptions involve a properly imposed thermodynamic limit as discussed in classical works of Khinchin [⁠30⁠ A. I. Khinchin, Analytical foundations of physical statistics. Russian Tracts on Advanced Mathematics and Physics, Vol. II, Gordon and Breach Publishers, New York; Hindustan Publishing (India), Delhi (1961) , ⁠31⁠ A. Y. Khinchin, Mathematical foundations of quantum statistics. Dover Publications, Mineola, NY (1998) ]. In practice, such equations are used at finite $k$ to describe real physical flows, but they are most likely incorrect even qualitatively in the opposite limit of large $k$. One notes also that the macroscopic fluid velocity is not an average over some small volume but is actually a statistical average of molecular velocity with a one-particle distribution function which is generally smooth. Thus, the average velocity is also smooth at small scales and can behave violently only on the macroscopic scale. Therefore, any solutions of these equations that vary strongly on smaller and smaller scale are simply outside the limit of applicability of these macroscopic equations and are of purely mathematical significance. They do not have any direct relation to real physical flows.

This situation can be illustrated by a simple example from liquid crystals (my field of expertise; in this example this is elasticity but in the hydrodynamics the situation is similar). Indeed, continuum equations of elasticity of nematic liquid crystals yield point singularities in the orientational director field which correspond to point defects observed in real systems. However, continuum theory cannot describe the radius of the defect core as there is no length scale. In fact, the defect core has finite radius which is calculated approximately from a statistical theory.

It is possible to obtain formal mathematical solutions of the continuum equations for the director distribution sufficiently close to the point discontinuity. However, these solutions have no relation to the real physical defect because in this domain we are inside the finite defect core with a completely different structure. The macroscopic theory simply breaks down because of large gradients which increase on approach to the singularity and the mathematically correct solutions in this domain lose their physical validity because they are obtained outside the range of validity of the continuum equations. One has to describe the system in this domain within a different framework of a molecular statistical theory which yields the results which correspond to the experiment.

3 Discussion

We suggest that the Buckmaster–Vicol theorem can be viewed in three main ways.

The first is that the result is solely of mathematical interest and whether or not it has physical relevance is of no concern. It is unnecessary to consider the requirements of fluid dynamics. It is only essential that the result is rigorously proved.

The second way is to accept that the result is a contribution to fluid dynamics but the implications, especially in relation to turbulence, are not yet fully understood. What, for example, is the connection to the work of Kolmogorov and Onsager? A discussion of this aspect is presented by De Lellis and Székelyhidi in [⁠16⁠ C. De Lellis and L. Székelyhidi, Jr., On turbulence and geometry: from Nash to Onsager. Notices Amer. Math. Soc. 66, 677–685 (2019) ].

The third point of view accepts that the Buckmaster–Vicol results might have no physical relevance. The difficulty here is that there are many potential reasons for this lack of physical relevance, by which again we mean observability in nature or in experiments, and some of these are discussed below. Being able to rule out some of the reasons and deciding between the ones that still remain (if any), appears to be an important task for mathematics, physics, and the philosophy of science. In particular, we assert that this debate is a fruitful one for philosophy of science in its rôle as the logic inspector of the scientific enterprise, and that issues raised in this particular debate have a broader domain of application.⁠³⁠An example would be a discussion of the gelation phenomenon in coagulation-fragmentation equations derived under the assumption of solute diluteness.

Below we shall briefly review what seem to us as, for now, legitimate reasons to doubt physical relevance of the Buckmaster–Vicol result. The list is as exhaustive as we could make it; we can envisage it becoming both longer and shorter in the future: longer due to the failure of our imagination, and shorter as arguments become available to rule out some of the possible grounds for criticism.

3.1 Classification of reasons

The possible reasons for lack of physical relevance are of different levels of depth. At the “shallowest” (not used pejoratively) end of the spectrum are grounds that agree with the approach and its use of the object of enquiry (the Navier–Stokes equations), but find fault with the result itself in the sense of not accepting the wild solutions obtained as being of physical relevance. At the next level of depth lie objections that have to do with the applicability of convex integration to the specific object of interest. The deepest objections have to do with the structure of matter (fluids in particular) at very short scales that the convex integration technique as a technique of analysis, does not respect a priori.

3.2 Result-level reasons

Here we are dealing with arguments that accept that the convex integration techniques can be applied to the Navier–Stokes equations but still find the results (such as the Buckmaster–Vicol theorem) wanting in physical plausibility.

As an example of such an argument, let us consider admissibility criteria. While there certainly are wild solutions that satisfy the entropy admissibility criterion [⁠37⁠ S. Markfelder, Convex integration applied to the multi-dimensional compressible Euler equations. Lecture Notes in Math. 2294, Springer, Cham (2021) ], there is not one known instance of a situation where any admissibility criterion yields a unique preferred wild solution. This is trivially true as wild solutions are created in physically indistinguishable (uncountable) equivalence classes. Hence, if one accepts that there should exist a mechanism that selects a unique solution of the Cauchy problem, such a mechanism will never select a wild solution; see for example the discussion in [⁠25⁠ H. Gimperlein, M. Grinfeld, R. J. Knops and M. Slemrod, The least action admissibility principle. Arch. Ration. Mech. Anal. 249, article no. 22 (2025) ].

However, first of all, this suggestion invites the rejoinder that there is no a priori binding principle that requires such a property of solutions in order to force uniqueness; perhaps “God plays dice” at the macro-level. At the same time, the question arises why in all known cases even equivalence classes of wild solutions do not satisfy admissibility criteria. In other words, at this level objections are consequences of objections at a deeper level.

Another point of view, articulated in the contributions by Kreml and by Markfelder, is that the concept of weak solution is not appropriate here. Again, the questions arise why this framework, so often productively used in PDEs, is inappropriate in the particular case of Navier–Stokes equations and what other framework (measure value solutions, or considering ensembles of weak solutions as opposed to working with individual ones) should come to replace it.

3.3 Object-level reasons

In this class of reasons one claims that the possible physical implausibility of results such as the Buckmaster–Vicol theorem follows from flaws in the Navier–Stokes equations and/or the application of convex integration techniques to it. This class naturally splits in two.

For the first subclass, one could claim that convex integration is applicable but that the flaw lies in the Navier–Stokes equations themselves, and that there exists another version of the equations, e.g., one involving thermal noise modifications as advocated by Eyink and Goldenfeld, or incorporating higher-order spatial terms or nonlocal/peridynamics ones, in which results would be more intuitively realistic.

In the rest of this subsection and in the next one we discuss arguments based on the conviction that the convex integration techniques should not be in principle applied to inter alia the Navier–Stokes equations or any other continuum formulation of laws of fluid motion; see also the contributions by Karlin and Kogelbauer and by Osipov.

To do that we need a one-sentence summary of the convex integration technique; the reader should consult [⁠37⁠ S. Markfelder, Convex integration applied to the multi-dimensional compressible Euler equations. Lecture Notes in Math. 2294, Springer, Cham (2021) ] for all the necessary definitions and details. It is this: starting with a suitable initial function (a sub-solution of an equation), we iteratively obtain a (family of) weak solutions to the equation in question in the limit by corrugating the sub-solution at ever decreasing scales.

It is therefore debatable if modifications at every scale can be made to a solution representing the velocity of a fluid, i.e., one may ask what it means for two such solutions to differ at the sub-Planck length scale. Observe that the incompressibility condition that assumes a well-defined macro-variable (density) and the definition of viscosity (that involves density as well) do not make sense at too short scales [⁠29⁠ N. Kavokine, R. R. Netz and L. Bocquet, Fluids at the nanoscale: from continuum to subcontinuum transport. Annu. Rev. Fluid Mech. 53, 377–410 (2021) ].

The main question that arises here is how an equation derived by making the assumption of continuum can be manipulated at scales where the assumption no longer holds.

Note that the formal object of enquiry bears no indication of the cut-off scales beyond which it cannot be manipulated.

We also observe that any analysis, such as the fundamental work of Onsager [⁠40⁠ L. Onsager, Statistical hydrodynamics. Nuovo Cimento (9) 6, 279–287 (1949) ], that assumes that the velocity field contains information about the flow at all scales, appears open to the same criticism. See [⁠20⁠ G. Eyink, Onsager’s ‘ideal turbulence’ theory. J. Fluid Mech. 988, article no. P1 (2024) , ⁠21⁠ G. L. Eyink and L. Peng, Space-time statistical solutions of the incompressible Euler equations and Landau–Lifshitz fluctuating hydrodynamics. arXiv:2409.13103v1 (2024) ] for a defence against this criticism.

This argument may harbour a hint to what concept of solution is appropriate for matter made of atoms and voids that is being analysed using a continuum description.

3.4 Structure of matter level reasons

The real numbers $\mathbb{R}$ provide a suitable setting for differential geometry, which is scale-free. However, it is arguable that a description of matter needs a fundamentally discrete setting at very short length scales (Planck length is of order $10^{-35}$ m and Planck time is of order $10^{-42}$ s). Without entering into details, we quote C. J. Isham [⁠28⁠ C. J. Isham, Topos methods in the foundations of physics. In Deep beauty: Understanding the quantum world through mathematical innovation, pp. 187–205, Cambridge Univ. Press, Cambridge (2011) , p. 189]:

The general assumption is that something “dramatic” happens to the nature of space and time at these fundamental scales. Precisely what that dramatic change might be, has been the source of endless speculation and conjecture. However, there is a fairly widespread anticipation that insofar as spatiotemporal concepts have any meaning at all in the “deep” quantum-gravity regime, the appropriate mathematical model will not be based on standard, continuum differential geometry.

3.5 Final remarks

We are aware that not all the possible views on the subject have been presented. Hence, reader comments and opinions are welcome, for example, on computational aspects of wild solutions. These comments can be sent to m.grinfeld@strath.ac.uk. If a lively debate ensues, a continuation paper on the subject will be considered by the EMS Magazine.

Gregory Eyink did undergraduate studies in mathematics and philosophy and earned his PhD in physics at the Ohio State University in 1987. Since 2003 he has been a Professor in Applied Mathematics and Statistics at the Johns Hopkins University, with joint appointments in Physics and Astronomy, in Mathematics and in Mechanical Engineering. His research interests include statistical physics, astrophysics, geophysics, condensed matter, fluid mechanics, dynamical systems, and partial differential equations. eyink@jhu.edu Heiko Gimperlein is a Professor of Mathematics at the University of Innsbruck. His research interests include topics in the numerical analysis and analysis of partial differential equations, including their applications in the natural sciences. heiko.gimperlein@uibk.ac.at Nigel Goldenfeld received his PhD in theoretical physics from the University of Cambridge (UK) in 1982, and in 1985 joined the faculty in the Department of Physics, University of Illinois at Urbana-Champaign, where he was for 36 years. He is currently on the faculty at the University of California San Diego. His research interests include fluid turbulence, renormalization group theory, singular perturbation theory and pattern formation. He is a Member of the National Academy of Sciences (US) and a Fellow of the Royal Society (UK). nigelg@ucsd.edu Michael Grinfeld completed his PhD in Mathematics at the Rensselaer Polytechnic Institute, Troy, N.Y., USA, working under the supervision of Marshall Slemrod. Since 1994 he has been at the University of Strathclyde in Glasgow doing research in differential equations applied to material science, as well as in economics and biomathematics. m.grinfeld@strath.ac.uk Ilya Karlin heads the Computational Kinetics Group at ETH Zurich. His expertise covers methods of model reduction with applications to kinetic theory and Boltzmann equation, polymer dynamics and chemical kinetics. He is key developer of the lattice Boltzmann method for fluid dynamics and inventor of the Entropic Lattice Boltzmann Method, which opened a door to high performance computation of turbulent flows. Ilya is recipient of two European Research Council Advanced Grants (2011 and 2018). His current research is focused on hypersonic flows along the Particles-on-Demand method. ikarlin@ethz.ch Robin J. Knops is Emeritus Professor of Mathematics, Heriot-Watt University, Edinburgh. His research interests are in qualitative properties of solutions to differential equations of continuum mechanics. r.j.knops@hw.ac.uk Florian Kogelbauer obtained his PhD in applied mathematics at the University of Vienna in 2016 and is currently a senior scientist at ETH Zurich. His research interests include geometric methods in dynamical systems, general fluid mechanics and kinetic theory with a focus on rigorous hydrodynamics derived from the Boltzmann equation. floriank@ethz.ch Ondřej Kreml is a researcher in the field of the analysis of PDEs describing fluid flows. He earned his PhD in 2010 from Charles University in Prague. He spent a year as a postdoctoral researcher at the University of Zurich, where he worked with Camillo De Lellis and Elisabetta Chiodaroli. He is a co-author of several papers on the existence of infinitely many admissible weak solutions to the compressible Euler system. kreml@math.cas.cz Colin McLarty is the Truman Handy Professor of Philosophy, and Professor of Mathematics, at Case Western Reserve University. He has worked in logic and the foundations of mathematics, with focus on the foundations of cohomological number theory. His work in the history and philosophy of mathematics runs from Poincaré and Hilbert, through Noether, Mac Lane, Grothendieck, and Lawvere, and recently philosophic issues of functional analysis and especially the Navier–Stokes equations. He has used all of that in connection with discussion of AI proof assistants. colin.mclarty@case.edu Simon Markfelder completed his PhD in mathematics in 2020 at the University of Würzburg, Germany. Afterwards he held postdoc positions at the University of Cambridge, UK, and the University of Würzburg. Currently, he is a junior professor for partial differential equations of mathematical physics at the University of Konstanz, Germany. He has published several papers on the theory of partial differential equations of mathematical fluid mechanics, as well as a monograph on convex integration. simon.markfelder@uni-konstanz.de Mikhail Osipov received his PhD in theoretical physics of condensed matter from the Moscow State University in 1983. He was an Alexander von Humboldt fellow in Germany and an invited professor or a guest researcher in Japan, Sweden, Portugal and France. He is a Professor of Applied Mathematics at the University of Strathclyde in Glasgow since 2000. M. Osipov is a leading expert in molecular statistical theory of liquid crystals, mesogenic polymers and related soft matter materials. m.osipov@strath.ac.uk Marshall Slemrod is a Professor Emeritus at the Department of Mathematics, University of Wisconsin, Madison, WI, USA. Prior to Wisconsin, Slemrod was a faculty member at Rensselaer Polytechnic Institute, Troy, NY, USA. He has PhD in applied mathematics from Brown University (1969) and SB in mathematics from the Massachusetts Institute of Technology (1965). slemrod@math.wisc.edu

1. ¹

   Here and in Section ⁠3⁠ “we” means H. Gimperlein, M. Grinfeld, R. J. Knops and M. Slemrod.

2. ²

   Kuhn refined his terminology in later editions, but we can use the original.

3. ³

   An example would be a discussion of the gelation phenomenon in coagulation-fragmentation equations derived under the assumption of solute diluteness.

References

1. F. Flandoli, An introduction to 3d stochastic fluid dynamics. In SPDE in hydrodynamic: recent progress and prospects. Lecture Notes in Math. 1942, pp. 51–150, Springer, Berlin; Fondazione C.I.M.E., Florence (2008)
2. J. J. Alibert and G. Bouchitté, Non-uniform integrability and generalized Young measures. J. Convex Anal. 4, 129–147 (1997)
3. D. Bandak, N. Goldenfeld, A. A. Mailybaev and G. Eyink, Dissipation-range fluid turbulence and thermal noise. Phys. Rev. E 105, article no. 065113 (2022)
4. D. Bandak, A. A. Mailybaev, G. L. Eyink and N. Goldenfeld, Spontaneous stochasticity amplifies even thermal noise to the largest scales of turbulence in a few eddy turnover times. Phys. Rev. Lett. 132, article no. 104002 (2024)
5. C. Bardos, F. Golse and C. D. Levermore, Fluid dynamic limits of kinetic equations. II. Convergence proofs for the Boltzmann equation. Comm. Pure Appl. Math. 46, 667–753 (1993)
6. J. Bedrossian and V. Vicol, The mathematical analysis of the incompressible Euler and Navier–Stokes equations: an introduction. Grad. Stud. Math. 225, American Mathematical Society, Providence, RI (2022)
7. J. B. Bell, A. Nonaka, A. L. Garcia and G. Eyink, Thermal fluctuations in the dissipation range of homogeneous isotropic turbulence. J. Fluid Mech. 939, article no. A12 (2022)
8. L. Bertini, A. De Sole, D. Gabrielli, G. Jona-Lasinio and C. Landim, Macroscopic fluctuation theory. Rev. Modern Phys. 87, 593–636 (2015)
9. D. Breit, E. Feireisl and M. Hofmanová, Solution semiflow to the isentropic Euler system. Arch. Ration. Mech. Anal. 235, 167–194 (2020)
10. T. Buckmaster and V. Vicol, Nonuniqueness of weak solutions to the Navier–Stokes equation. Ann. of Math. (2) 189, 101–144 (2019)
11. T. Buckmaster and V. Vicol, Convex integration constructions in hydrodynamics. Bull. Amer. Math. Soc. (N.S.) 58, 1–44 (2021)
12. S. Daneri, E. Runa and L. Székelyhidi, Non-uniqueness for the Euler equations up to Onsager’s critical exponent. Ann. PDE 7, article no. 8 (2021)
13. C. De Lellis and H. Kwon, On nonuniqueness of Hölder continuous globally dissipative Euler flows. Anal. PDE 15, 2003–2059 (2022)
14. C. De Lellis and L. Székelyhidi, Jr., The Euler equations as a differential inclusion. Ann. of Math. (2) 170, 1417–1436 (2009)
15. C. De Lellis and L. Székelyhidi, Jr., On admissibility criteria for weak solutions of the Euler equations. Arch. Ration. Mech. Anal. 195, 225–260 (2010)
16. C. De Lellis and L. Székelyhidi, Jr., On turbulence and geometry: from Nash to Onsager. Notices Amer. Math. Soc. 66, 677–685 (2019)
17. R. J. DiPerna, Measure-valued solutions to conservation laws. Arch. Rational Mech. Anal. 88, 223–270 (1985)
18. J. Duchon and R. Robert, Inertial energy dissipation for weak solutions of incompressible Euler and Navier–Stokes equations. Nonlinearity 13, 249–255 (2000)
19. T. Elgindi, Finite-time singularity formation for C1,α solutions to the incompressible Euler equations on \mathbb⁢R3. Ann. of Math. (2) 194, 647–727 (2021)
20. G. Eyink, Onsager’s ‘ideal turbulence’ theory. J. Fluid Mech. 988, article no. P1 (2024)
21. G. L. Eyink and L. Peng, Space-time statistical solutions of the incompressible Euler equations and Landau–Lifshitz fluctuating hydrodynamics. arXiv:2409.13103v1 (2024)
22. E. Feireisl, A. Jüngel and M. Lukáčová-Medvid’ová, Maximal dissipation and well-posedness of the Euler system of gas dynamics. arXiv:2501.05134v2 (2025)
23. G. P. Galdi, An introduction to the mathematical theory of the Navier–Stokes equations: Steady-state problems. Second ed., Springer Monogr. Math., Springer, New York (2011)
24. B. Gess, D. Heydecker and Z. Wu, Landau–Lifshitz–Navier–Stokes equations: Large deviations and relationship to the energy equality. arXiv:2311.02223v2 ([v1] 2023, [v2] 2024)
25. H. Gimperlein, M. Grinfeld, R. J. Knops and M. Slemrod, The least action admissibility principle. Arch. Ration. Mech. Anal. 249, article no. 22 (2025)
26. F. Golse and L. Saint-Raymond, The Navier–Stokes limit of the Boltzmann equation for bounded collision kernels. Invent. Math. 155, 81–161 (2004)
27. M. L. Gromov, Convex integration of differential relations. I. Izv. Akad. Nauk SSSR Ser. Mat. 37, 329–343 (1973)
28. C. J. Isham, Topos methods in the foundations of physics. In Deep beauty: Understanding the quantum world through mathematical innovation, pp. 187–205, Cambridge Univ. Press, Cambridge (2011)
29. N. Kavokine, R. R. Netz and L. Bocquet, Fluids at the nanoscale: from continuum to subcontinuum transport. Annu. Rev. Fluid Mech. 53, 377–410 (2021)
30. A. I. Khinchin, Analytical foundations of physical statistics. Russian Tracts on Advanced Mathematics and Physics, Vol. II, Gordon and Breach Publishers, New York; Hindustan Publishing (India), Delhi (1961)
31. A. Y. Khinchin, Mathematical foundations of quantum statistics. Dover Publications, Mineola, NY (1998)
32. F. Kogelbauer and I. Karlin, Rigorous hydrodynamics from linear Boltzmann equations and viscosity-capillarity balance. Phys. Rev. E 110, article no. 055105 (2024)
33. T. S. Kuhn, The structure of scientific revolutions. University of Chicago Press, Chicago (1962)
34. L. D. Landau and E. M. Lifshitz, Fluid mechanics. Course of Theoretical Physics, Vol 6, Pergamon Press, London–Paris–Frankfurt; Addison-Wesley Publishing, Reading, MA (1959)
35. P.-L. Lions and N. Masmoudi, From the Boltzmann equations to the equations of incompressible fluid mechanics. I. Arch. Ration. Mech. Anal. 158, 173–193 (2001)
36. P.-L. Lions and N. Masmoudi, From the Boltzmann equations to the equations of incompressible fluid mechanics. II. Arch. Ration. Mech. Anal. 158, 195–211 (2001)
37. S. Markfelder, Convex integration applied to the multi-dimensional compressible Euler equations. Lecture Notes in Math. 2294, Springer, Cham (2021)
38. C. McLarty, Fluid mechanics for philosophers, or which solutions do you want for Navier–Stokes? In Working toward solutions in fluid dynamics and astrophysics: What the equations don’t say, SpringerBriefs Hist. Sci. Technol., Springer, Cham, 31–56 (2023)
39. J. Nash, C1 isometric imbeddings. Ann. of Math. (2) 60, 383–396 (1954)
40. L. Onsager, Statistical hydrodynamics. Nuovo Cimento (9) 6, 279–287 (1949)
41. J. Quastel and H.-T. Yau, Lattice gases, large deviations, and the incompressible Navier–Stokes equations. Ann. of Math. (2) 148, 51–108 (1998)
42. M. Rorvig, Mathematicians identify threshold at which shapes give way. (2021) https://www.quantamagazine.org/mathematicians-identify-threshold-at-which-shapes-give-way-20210603
43. J. Serrin, The initial value problem for the Navier–Stokes equations. In Nonlinear Problems (Proc. Sympos., Madison, Wis., 1962), Univ. Wisconsin Press, Madison, WI, 69–98 (1963)
44. A. Shnirelman, On the non-uniqueness of weak solution of the Euler equations. In Journées équations aux dérivées partielles, article no. 18 (1996)
45. T. C. Sideris, Formation of singularities in three-dimensional compressible fluids. Comm. Math. Phys. 101, 475–485 (1985)
46. L. M. Silverman and B. D. O. Anderson, Controllability, observability and stability of linear systems. SIAM J. Control 6, 121–130 (1968)
47. C. Truesdell and R. G. Muncaster, Fundamentals of Maxwell’s kinetic theory of a simple monatomic gas: Treated as a branch of rational mechanics. Pure Appl. Math. 83, Academic Press, Harcourt Brace Jovanovich, Publishers, New York–London (1980)
48. C. Villani, Paradoxe de Scheffer–Shnirelman revu sous l’angle de l’intégration convexe (d’après C. De Lellis et L. Székelyhidi). Astérisque 332, article no. 1001 (2010)
49. Z. Xin, Blowup of smooth solutions to the compressible Navier–Stokes equation with compact density. Comm. Pure Appl. Math. 51, 229–240 (1998)
50. J. M. O. de Zárate and J. V. Sengers, Hydrodynamic fluctuations in fluids and fluid mixtures. Elsevier, Amsterdam (2006)