Wikimedia and zbMATH Open share a vision of open knowledge accessible to all. While Wikimedia’s mission is to provide a broad audience with an overview of well-established knowledge, zbMATH Open is oriented toward new knowledge for working mathematicians. In this article, we describe the intersection of these two platforms, compare their mathematical formula presentation methods, and outline future directions to deepen collaboration between them.

1 Introduction

Open platforms like Wikimedia (including Wikipedia, Wikidata, and many more) and zbMATH Open provide moderated spaces tailored to their respective communities. While differing in culture, policies, and content curation practices, each community creates their unique habitat and generates digital objects. These digital outputs might be of value to other communities, and thus linking similar content in different digital spaces has huge benefits.

Wikimedia has a broader range of audience than zbMATH Open (which is a platform exclusively dedicated to mathematical data). Yet, Wikipedia has a large and active community of contributors with a strong subcommunity of mathematics editors [⁠3⁠ D. Eppstein, J. B. Lewis and R. Woodroofe, Princ-wiki-a mathematica: Wikipedia editing and mathematics. Notices Amer. Math. Soc. 72, 65–73 (2025) ]. Aimed at a wider range of audiences, Wikimedia has its weaknesses and strengths, especially when it comes to presentation of mathematical formulae. For instance, Wikipedia misses some depth in certain mathematical fields. Wikipedia articles use references to scientific papers and, in rare cases, links to zbMATH Open or MathSciNet reviews of those papers and support this by reference macros. A further challenge arises from the inconsistency in notation and even content in different language versions of Wikipedia. The vision of a semi-formal, language-independent Wiki [⁠2⁠ J. Corneli and M. Schubotz, math.wikipedia.org: A vision for a collaborative, semi-formal, language independent math(s) encyclopedia. In Proceedings for AITP 2017: The Second Conference on Artificial Intelligence and Theorem Proving, pp. 28–31 (2017) ] has not yet materialised.

Despite these limitations, Wikimedia has its strengths as an open platform for mathematical data. For example, the Encyclopedia of Mathematics⁠1⁠https://encyclopediaofmath.org uses the same Wiki software (albeit under a different license and editorial policies regarding who can contribute and how) and focuses on mathematics. In addition, Wikimedia’s central database, Wikidata, holds a large amount of curated information on authors and publications, which are cross-referenced with zbMATH Open.

Although Wikimedia and zbMATH Open differ, both platforms support mathematical formulae as an integral part of the text content. Therefore, the presentation of mathematical formulae and the rendering methods play an important role for both Wikimedia and zbMATH Open. This is an important area where both platforms can be interlinked and use each other’s presentation methods. We will delve further into this in the following sections.

In this article, we will address:

  1. the connections between Wikimedia projects and zbMATH Open,

  2. a comparison of mathematical formulae rendering methods,

  3. plans to deepen the integration of the two platforms.

2 Linking Wikimedia and zbMATH Open

In this section, we discuss some shared entities across Wikimedia and zbMATH Open, emphasising author/public figure profiles. Other shared entities, such as conferences and journals, are essentially similar to public figure profiles in structure and function. Although Wikimedia and zbMATH Open may have different content and use different technologies for presenting those shared entities, the overlap provides opportunities for mutual benefits. We give examples and statistics showing how the two platforms benefit from each other. We briefly introduce Mathematical Research Data Initiative (MaRDI), a platform that uses Wikimedia’s technology, but the content from zbMATH Open and similar platforms that are specialised in mathematical content. We conclude this section by presenting some facts and statistics on a framework that is used for connecting platforms via mathematical entity linking.

2.1 Connecting and improving common entities

A frequently shared content type in both zbMATH Open and Wikimedia projects is the public figures profiles. In zbMATH Open, mathematicians’ profiles focus on zbMATH Open-indexed related documents – as authors, editors, subjects, or reviewers. These links allow statistics, timelines, and networks of co-authorship and co-co-authorship to be computed and visualised.

A mathematician covered in zbMATH Open might be missing in the Wikimedia ecosystem due to different criteria for public figures and the broader scope of Wikimedia, which often includes biographical information and extracurricular details. Additionally, a public figure may appear on several Wikimedia pages and its sister platforms, such as the multilingual platforms Wikidata and Wikimedia Commons, the various language versions of Wikipedia, Wikisource, Wikiquote and so on.

Despite structural differences, the Wikimedia ecosystem and zbMATH Open share similarities in handling public figure profiles. For example, both platforms link to external resources such as Open Researcher and Contributor ID (ORCID) or the Mathematics Genealogy Project (MGP).⁠2⁠https://mathgenealogy.org

Beyond public figures, entities such as software, journals, conferences, and theorems appear on both zbMATH Open and Wikimedia. Similarly to public figure profiles, zbMATH Open has dedicated and more structured pages for publications, journals, and software, while Wikimedia provides a broader, albeit less comprehensive, coverage. Different approaches to shared entities on the two platforms can be considered complementary and provide room to link and improve each other.

Disambiguation is crucial for creating and maintaining content for public figure profiles, journals, etc. Both communities have developed workflows for resolving ambiguity, using different approaches, which are continuously being refined. Such disambiguation workflows benefit from expertise in relevant mathematical fields, linguistics (e.g., concerning naming conventions in certain cultures), bibliographic data and potentially other fields, for which diversity in the curator community is helpful. As the result of a disambiguation process often manifests itself in distinct links to external resources, the mutual links between zbMATH Open and Wikimedia platforms foster quality assessment and coordination.

While the advantages of disambiguation are clear, challenges remain, which often require manual corrections by experts. Several dedicated tools for profiling and disambiguating scholarly entities have been developed in Wikidata, such as Scholia [⁠10⁠ F. Å. Nielsen, D. Mietchen and E. Willighagen, Scholia and scientometrics with wikidata. In The Semantic Web: ESWC 2017 Satellite Events. ESWC 2017, pp. 237–259, †Lecture Notes in Comput. Sci. 10577, Springer, Cham, (2017) ], the Author Disambiguator⁠3⁠https://author-disambiguator.toolforge.org/ and the ORCID Scraper.⁠4⁠https://orcid-scraper.toolforge.org/

The author identity workflow and the disambiguation process of the profiles in zbMATH Open have been investigated in [⁠8⁠ H. Mihaljević-Brandt and N. Roy, zbMATH author profiles: open up for user participation. Eur. Math. Soc. Newsl. 93, 53–55 (2014) , ⁠11⁠ N. D. Roy, Author identification through and for interconnectivity: a brief history of author identification at zbMATH Open. In 90 years of zbMATH, pp. 43–48, European Mathematical Society (EMS), Berlin (2024) ]. As an example of the content exchange between Wikimedia and zbMATH Open on authors, Wikidata Q IDs for zbMATH Open authors are listed automatically and manually. Currently, there are 75641 Wikidata IDs listed in zbMATH Open profiles – 15740 manually and 59901 automatically. Other than author data, various other information is harvested constantly from Wikidata, e.g., 2874 bio-events come from Wikidata. For transparency, the source of information is clarified in zbMATH Open.

Obviously, such an interconnected framework has significant advantages, since information, corrections, and data improvements can be shared among the platforms. However, such a system must be carefully curated to minimise error propagation. For instance, due to a raw ingest of data from MGP, there are many duplicated identifiers for mathematicians in Wikipedia (though some of them have been merged since then, often along with zbMATH Open curation). Many people have several registered ORCIDs, as well as some ORCIDs encompassing many people. Manual curation has also shown a surprising amount of improper ID matching between MGP and MathSciNet for ambiguous names. Even completely correct ID matches may be spoiled by future misassignments.

Therefore, beyond automated sanity checks, such a framework constantly needs feedback and corrections from the community, which is relatively easily possible through the corresponding interfaces in Wikipedia and zbMATH Open.

2.2 Mathematical Research Data Initiative (MaRDI)

An initiative to systematically profile mathematical entities of various types is currently underway at MaRDI.⁠5⁠https://mardi4nfdi.de/ the Mathematical Research Data Initiative [⁠17⁠ The MaRDI consortium, Mardi: Mathematical research data initiative proposal (2022) ] that forms the mathematical arm of Germany’s National Research Data Infrastructure (NFDI),⁠6⁠https://nfdi.de/ MaRDI operates a portal⁠7⁠https://portal.mardi4nfdi.de/ that provides information about various types of mathematical entities, from mathematical publications to mathematicians, formulae, algorithms, theorems and beyond.

The technical setup of the portal [⁠14⁠ M. Schubotz, E. Ferrer, J. Stegmüller, D. Mietchen, O. Teschke, L. Pusch and T. Conrad, Bravo MaRDI: A wikibase knowledge graph on mathematics. In Proceedings of the Wikidata Workshop 2023 (2025). https://ceur-ws.org/Vol-3640/paper3.pdf] is closely aligned with that of Wikidata. MaRDI also operates a fork of Scholia and is building Scholia-inspired profiles that reside on the portal wiki and are automatically generated based on the information the portal has about the entity to be profiled (e.g., a publication), as well as related ones (e.g., that publication’s authors). Whenever possible, such profiles link to zbMATH Open, Wikidata, and other relevant resources, such as DBLP Computer Science Bibliography. This can serve as a fertile ground for coordinating curation workflows regarding the profiled entities. MaRDI can be considered as an example of interaction between zbMATH Open and Wikimedia, built on top of the Wikimedia set-up, although content-wise closer to zbMATH Open.

2.3 Connecting platforms through mathematical entity linking

In [⁠6⁠ M. Fuhrmann, P. Scharpf and M. Schubotz, Entity linking for zbMATH open. Eur. Math. Soc. Mag. 134, 61–63 (2024) ] a framework is described for a phrase-based entity linking at zbMATH Open. Since then, it has been applied to generate links to four platforms: Wikipedia, Encyclopedia of Mathematics, NLab,⁠8⁠https://ncatlab.org/ and Wolfram MathWorld.⁠9⁠https://mathworld.wolfram.com/ While all links are made available via the zbMATH Open API [⁠5⁠ M. Fuhrmann and F. Müller, A REST API for zbMATH Open access. Eur. Math. Soc. Mag. 130, 63–65 (2023) ], the zbMATH Open interface currently displays only a fraction of them for user convenience: Common elementary phrases, which are assumed to be familiar to zbMATH Open users, are not linked explicitly. However, their availability in the API enables a wide range of possible applications, such as reusability in knowledge graphs, backlinking from the platforms, recommender systems, or automated classification [⁠15⁠ M. Schubotz, P. Scharpf, O. Teschke, A. Kühnemund, C. Breitinger and B. Gipp, AutoMSC: automatic assignment of Mathematics Subject Classification labels. In Intelligent computer mathematics. 13th international conference, CICM 2020, Bertinoro, Italy, July 26–31, 2020. Proceedings, pp. 237–250, Springer, Cham (2020) ]. Certainly, more applications deriving from this will be implemented in the future and discussed in detail in forthcoming columns.

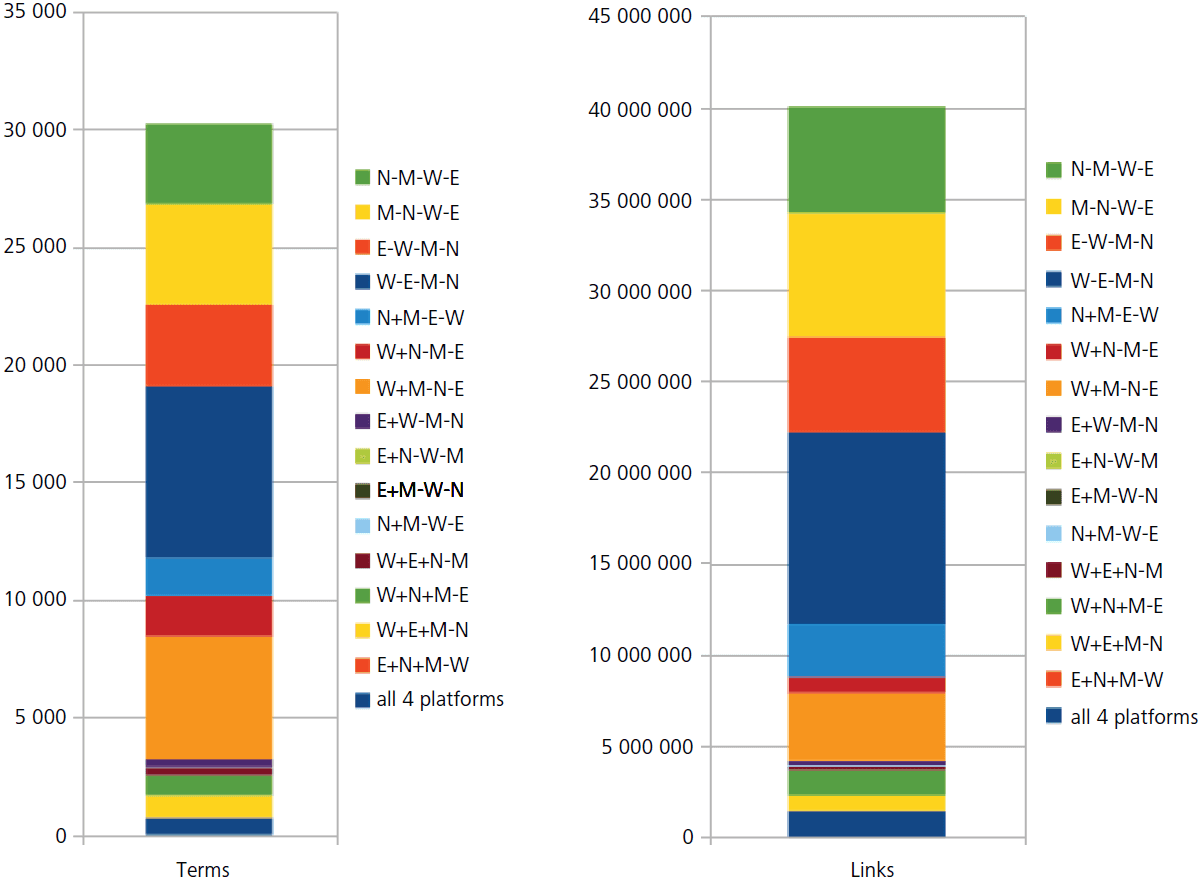
To give a brief impression about the scope and overlap of the platforms and the frequency of their phrases occurring in the mathematical literature, in Figure ⁠1⁠ we illustrate with a statistic the distribution of the currently identified 40 027 388 links to 30 216 unique phrases from the four services.

Figure 1. Distribution of terms and links from zbMATH Open to four different vocabularies: Wikipedia (W), Encyclopedia of Mathematics (E), NLab (N), and MathWorld (M) and their intersections.

We can observe some effects here: Most links, as well as most phrases, come from Wikipedia alone (naturally, since it has the largest vocabulary), although with a reduced frequency. On the other hand, entries from NLab (individually or when included on other platforms) occur much more frequently in research-level mathematics.

3 Mathematical formulae

Mathematical typesetting is an essential part of the presentation of mathematical knowledge. TEX (and LATEX) has been the main typesetting tool among mathematicians for decades due to its flexibility and precision. However, LATEX has several limitations when used in web-based environments such as zbMATH Open, particularly regarding consistency, long-term stability, and machine readability.

In this section, we compare the mathematical formula rendering methods in Wikimedia and zbMATH Open. We briefly introduce WikiTexVC [⁠12⁠ M. Schubotz, texvc (LaTeX package). (2018), [v1.2] (2020) , ⁠16⁠ J. Stegmüller and M. Schubotz, WikiTexVC: MediaWiki’s native LaTeX to MathML converter for Wikipedia. arXiv:2401.16786v1 (2024) ], the grammar-based method used in Wikimedia, and propose adapting a grammar-based presentation in zbMATH Open.

3.1 Formula rendering: Wikimedia vs. zbMATH Open

In Wikimedia, mathematical formulae are handled via the Math extension using WikiTexVC [⁠12⁠ M. Schubotz, texvc (LaTeX package). (2018), [v1.2] (2020) ], which is a grammar-based approach to parsing LATEX formulae into a structured internal representation and then translating them into MathML – a standard mathematical formula representation tool for the web. This approach creates a clear and consistent internal structure supporting long-term stability, semantic analysis, and interoperability (see [⁠13⁠ M. Schubotz, G.-P. André, N. Meuschke, O. Teschke and B. Gipp, Mathematical formulae in Wikimedia projects. In JCDL ’20: Proceedings of the ACM/IEEE Joint Conference on Digital Libraries in 2020, pp. 447–448, Association for Computing Machinery, New York (2020) ] for a discussion of some examples).

Traditional mathematical presentation methods follow a standard structure in mathematical logic that consists in a set of rules applied to the given set of variables and functions to generate mathematical expressions. This approach makes such systems expressive, and hence powerful, but at the same time ambiguous on occasions. In contrast, recognition-based systems such as parsing expression grammars (PEG) [⁠4⁠ B. Ford, Parsing expression grammars: a recognition-based syntactic foundation. In Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL ’04, pp. 111–122, Association for Computing Machinery, New York (2004) ] that are used in WikiTexVC include rules that decide whether a given formula is well-formed. Recognition-based systems avoid ambiguity.

In contrast to Wikipedia, zbMATH Open previously used MathML for formula search [⁠1⁠ P. Baier and O. Teschke, Zentralblatt MATHMLized. Eur. Math. Soc. Newsl. 76, 55–57 (2010) , ⁠7⁠ M. Kohlhase, Mathematical knowledge management: transcending the one-brain-barrier with theory graphs. Eur. Math. Soc. Newsl. 92, 22–27 (2014) , ⁠9⁠ F. Müller and O. Teschke, Full text formula search in zbMATH. Eur. Math. Soc. Newsl. 102, 51 (2016) ] and display, now supplemented with MathJax. While MathML is an established standard for formula presentation on the web, its usage typically relies on external LATEX input that is parsed less systematically. This makes the input rely on many (custom) macros in LATEX, which can cause inconsistency, especially over time, problems with searchability and semantic interoperability.

WikiTexVC mitigates these issues by offering a canonical structure, as it handles almost all (if not all) standard LATEX macros. WikiTexVC also allows formulae to be rendered reliably and searched more effectively.

3.2 Grammar-based LATEX for zbMATH Open

Given the challenges faced by zbMATH Open in handling LATEX formulae, adopting a grammar-based presentation will provide several advantages.

  • Searchability: enhances easier search, even across variants.

  • Stability: ensures long-term interpretability for formulae, even years after publication without being affected by the macros version change.

  • Interoperability: facilitates content sharing between Wikipedia and zbMATH Open.

  • Longevity: allows durability, hence not being affected by obsolete or deprecated LATEX macros.

  • Balance between Machine Readability and Mathematical Expression: making formulae accessible to the machine and automated tools, easing parsing and mathematical content analysis.

WikiTexVC represents an alternative promising direction for web-based mathematical publishing. While implementation details used in parsing language grammar might not be of interest to all users, the long-term benefits of adapting WikiTeXVC to zbMATH Open for the mathematical community are clear.

Naturally, beyond phrases, a significant part of mathematical information is encoded in formulae. Automated extraction of relevant formula entities and interlinking them with the proper semantics is an even more sophisticated issue.

4 Conclusions

We discussed that Wikimedia and zbMATH Open have active communities, both of which engage in processing primary literature to enhance its reusability for their respective target audiences, the general public and professional mathematicians. While both platforms are open and their visions align, the links between them are limited. In this article, we presented ideas on sharing technology between the two platforms for rendering mathematical formulae and proposed future collaboration paths for improving connections. Strengthening these ties will benefit the mathematical community and digital communication at large.

Acknowledgements. This research was supported by the mathematical research-data initiative MaRDI, funded by the Deutsche Forschungsgemeinschaft (DFG), project number 460135501, NFDI 29/1 “MaRDI –- Mathematische Forschungsdateninitiative.”

Hamid Rahkooy is a researcher in mathematical information infrastructure at FIZ Karlsruhe – Leibniz Institute for Information Infrastructure, Berlin, Germany. He works on defining mathematical formulae on the web in the context of validating LATEX formulae from wiki texts and integrating them into MediaWiki. hamid.rahkooy@fiz-karlsruhe.de Moritz Schubotz studied physics and computer science at the University of Wuppertal and TU Berlin. After his PhD, he was a postdoc at the University of Konstanz and the National Institute of Informatics in Tokyo before joining FIZ Karlsruhe in 2019. At FIZ Karlsruhe, he researches methods to improve zbMATH Open and related research infrastructure. moritz.schubotz@fiz-karlsruhe.de Olaf Teschke studied mathematics at Humboldt University Berlin, and completed his PhD in algebraic geometry there. He moved to FIZ Karlsruhe in 2008, and has been working there since 2009 as the head of the Mathematics Department and managing editor of zbMATH (including a short intermediate term as editor-in-chief). He has also served in several EMS committee positions. His main occupation is information infrastructure for mathematics. olaf.teschke@fiz-karlsruhe.de Marcel Fuhrmann studied physics at Humboldt-Universität zu Berlin. He completed his PhD in astrophysics and worked as a postdoctoral researcher in applied mathematics at the University of Potsdam. From 2017 to 2021, he worked at the German Federal Institute for Risk Assessment. In 2021, he moved to FIZ Karlsruhe and worked on the zbMATH Open REST API and other related projects. marcel.fuhrmann@fiz-karlsruhe.de Nicolas Roy studied theoretical physics in Université Grenoble Alpes, in France, and then obtained a PhD in Mathematics in 2003. Afterwards, he came as postdoc to the Institut für Mathematik, at Humboldt-Universität zu Berlin, until end 2010. After a two-year period (2011-2012) working for the school adaptive learning system Bettermarks GmbH, he moved in 2013 to FIZ Karlsruhe, as a scientific editor and developer. He leads the author disambiguation system at zbMATH Open. nicolas.roy@fiz-karlsruhe.de Daniel Mietchen studied biophysics at Humboldt-Universität zu Berlin and completed a PhD in physics at Saarland University. Since then, he has been exploring methodological and infrastructural aspects of the life sciences and adjacent fields, through which he became interested in opening up scholarly workflows in general. At FIZ Karlsruhe since 2022, his current emphasis is on interconnecting mathematical knowledge and workflows with those in other research fields through semantic technologies, particularly knowledge graphs. daniel.mietchen@fiz-karlsruhe.de

  1. 1

    https://encyclopediaofmath.org

  2. 2

    https://mathgenealogy.org

  3. 3

    https://author-disambiguator.toolforge.org/

  4. 4

    https://orcid-scraper.toolforge.org/

  5. 5

    https://mardi4nfdi.de/

  6. 6

    https://nfdi.de/

  7. 7

    https://portal.mardi4nfdi.de/

  8. 8

    https://ncatlab.org/

  9. 9

    https://mathworld.wolfram.com/

References

  1. P. Baier and O. Teschke, Zentralblatt MATHMLized. Eur. Math. Soc. Newsl. 76, 55–57 (2010)
  2. J. Corneli and M. Schubotz, math.wikipedia.org: A vision for a collaborative, semi-formal, language independent math(s) encyclopedia. In Proceedings for AITP 2017: The Second Conference on Artificial Intelligence and Theorem Proving, pp. 28–31 (2017)
  3. D. Eppstein, J. B. Lewis and R. Woodroofe, Princ-wiki-a mathematica: Wikipedia editing and mathematics. Notices Amer. Math. Soc. 72, 65–73 (2025)
  4. B. Ford, Parsing expression grammars: a recognition-based syntactic foundation. In Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL ’04, pp. 111–122, Association for Computing Machinery, New York (2004)
  5. M. Fuhrmann and F. Müller, A REST API for zbMATH Open access. Eur. Math. Soc. Mag. 130, 63–65 (2023)
  6. M. Fuhrmann, P. Scharpf and M. Schubotz, Entity linking for zbMATH open. Eur. Math. Soc. Mag. 134, 61–63 (2024)
  7. M. Kohlhase, Mathematical knowledge management: transcending the one-brain-barrier with theory graphs. Eur. Math. Soc. Newsl. 92, 22–27 (2014)
  8. H. Mihaljević-Brandt and N. Roy, zbMATH author profiles: open up for user participation. Eur. Math. Soc. Newsl. 93, 53–55 (2014)
  9. F. Müller and O. Teschke, Full text formula search in zbMATH. Eur. Math. Soc. Newsl. 102, 51 (2016)
  10. F. Å. Nielsen, D. Mietchen and E. Willighagen, Scholia and scientometrics with wikidata. In The Semantic Web: ESWC 2017 Satellite Events. ESWC 2017, pp. 237–259, †Lecture Notes in Comput. Sci. 10577, Springer, Cham, (2017)
  11. N. D. Roy, Author identification through and for interconnectivity: a brief history of author identification at zbMATH Open. In 90 years of zbMATH, pp. 43–48, European Mathematical Society (EMS), Berlin (2024)
  12. M. Schubotz, texvc (LaTeX package). (2018), [v1.2] (2020)
  13. M. Schubotz, G.-P. André, N. Meuschke, O. Teschke and B. Gipp, Mathematical formulae in Wikimedia projects. In JCDL ’20: Proceedings of the ACM/IEEE Joint Conference on Digital Libraries in 2020, pp. 447–448, Association for Computing Machinery, New York (2020)
  14. M. Schubotz, E. Ferrer, J. Stegmüller, D. Mietchen, O. Teschke, L. Pusch and T. Conrad, Bravo MaRDI: A wikibase knowledge graph on mathematics. In Proceedings of the Wikidata Workshop 2023 (2025). https://ceur-ws.org/Vol-3640/paper3.pdf
  15. M. Schubotz, P. Scharpf, O. Teschke, A. Kühnemund, C. Breitinger and B. Gipp, AutoMSC: automatic assignment of Mathematics Subject Classification labels. In Intelligent computer mathematics. 13th international conference, CICM 2020, Bertinoro, Italy, July 26–31, 2020. Proceedings, pp. 237–250, Springer, Cham (2020)
  16. J. Stegmüller and M. Schubotz, WikiTexVC: MediaWiki’s native LaTeX to MathML converter for Wikipedia. arXiv:2401.16786v1 (2024)
  17. The MaRDI consortium, Mardi: Mathematical research data initiative proposal (2022)

Cite this article

Hamid Rahkooy, Moritz Schubotz, Olaf Teschke, Marcel Fuhrmann, Nicolas Roy, Daniel Mietchen, Wikipedia and zbMATH Open: Connecting several layers of mathematical information. Eur. Math. Soc. Mag. 136 (2025), pp. 59–63

DOI 10.4171/MAG/252
This open access article is published by EMS Press under a CC BY 4.0 license, with the exception of logos and branding of the European Mathematical Society and EMS Press, and where otherwise noted.
Back to Issue 136