Chaotic properties of smooth dynamical systems

1 Introduction

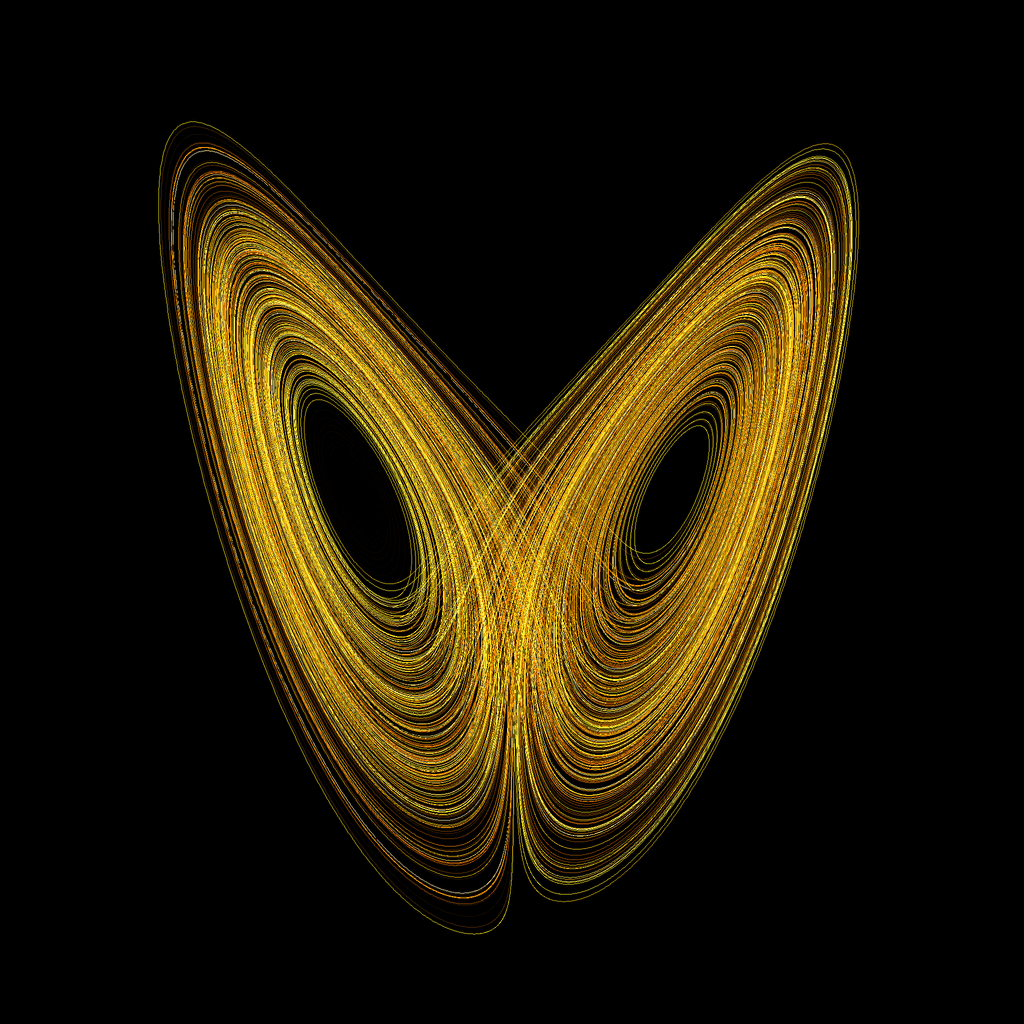
The fields of dynamical systems and ergodic theory are concerned with evolution of a given system under time. Given an initial condition (or a set of initial conditions) one is interested in its long term behavior. One of the founders of modern dynamical systems is Henri Poincaré. The famous Poincaré recurrence theorem [⁠47⁠ H. Poincaré, Sur le problème des trois corps et les équations de la dynamique. Acta Math. 13, 1–270 (1890) ] states that a measure-preserving dynamical system will return (infinitely often) arbitrarily close to its initial state. Subsequent fundamental achievements came with ergodic theorems, proven by John von Neumann in the $L^2$ setting [⁠41⁠ J. von Neumann, Proof of the quasi-ergodic hypothesis. Proc. Natl. Acad. Sci. USA 18, 70–82 (1932) ] and by George Birkhoff in a stronger almost everywhere situation [⁠3⁠ G. D. Birkhoff, Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA 17, 656–660 (1931) ]. They imply that, under the natural ergodicity assumption on the system, the time average is equal to the space average. In particular, they yield quantitative information on the set of return times in the Poincaré recurrence theorem. These theorems gave first general statements on random behavior in dynamics. This naturally sparked questions on what finer chaotic properties one can (typically) observe in naturally appearing dynamical systems, which became one of the central directions of study in the realm of (smooth) dynamical systems in the second half of the last century. More precisely, people were interested in random behavior of deterministic systems, i.e., in how sensitive can the evolution of a deterministic system be (depending on the initial condition). One of the main motivations was coming from dynamical systems modeling real-life phenomena, such as evolution of weather or motion of planets in the solar system. Most notably, in the 1960s Edward Lorenz [⁠38⁠ E. N. Lorenz, Deterministic nonperiodic flow. J. Atmospheric Sci. 20, 130–141 (1963) ], a meteorologist and mathematician, was conducting an experiment on predicting the weather in a given place on earth. He came up with a deterministic dynamical system modeling the evolution of weather and noticed that even a tiny perturbation of the initial condition would typically lead to a completely different outcome after a relatively short time. This phenomenon became known as the butterfly effect and this led to the discovery of the so-called (chaotic) Lorenz attractor (see Figure ⁠1⁠⁠¹⁠Taken from https://commons.wikimedia.org/wiki/File:Lorenz_system_r28_s10_b2-6666.png.).

At around the same time some fundamental mathematical tools were developed which allowed to rigorously measure randomness of deterministic dynamical systems. The entropy of an abstract measure-preserving system was defined by Kolmogorov and Sinai in the late 1950s [⁠35⁠ A. N. Kolmogorov, A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. (in Russian) Dokl. Akad. Nauk SSSR (N.S.) 119, 861–864 (1958) , ⁠56⁠ Ya. G. Sinaĭ, On the concept of entropy for a dynamic system. Dokl. Akad. Nauk SSSR (in Russian) 124, 768–771 (1959) ]. Systems with positive entropy would then exhibit strong randomness, at least in ‘parts’ of the system. Other fundamental objects defined for smooth systems on manifolds are the Lyapunov exponents. Positivity of Lyapunov exponents is another manifestation of strongly chaotic properties. There are also other qualitative and quantitative properties that yield a hierarchy of possible chaotic behaviors. By qualitative properties we mean properties that can be defined for an abstract dynamical system. Some main examples are: ergodicity, weak mixing, mixing, absolutely continuous spectrum, positive entropy, $K$-property and Bernoulli property. Quantitative properties use some additional structure of the system (in most cases smooth or piecewise-smooth structure). Some main examples are: rates of deviation of ergodic averages, rates of weak mixing and mixing (decay of correlations), central limit theorem, large deviations. The last seventy years have seen a spectacular development in studying chaotic properties of (smooth) dynamical systems. In the sections below I plan to give a selective account of some important classical results in the theory, highlight some of the more recent developments, and discuss some open problems and future directions.

2 Randomness in deterministic systems

One of the fundamental discoveries in smooth dynamical systems in the last seventy years is the fact that deterministic (smooth) dynamical systems can behave very randomly. In particular, in many aspects such systems can behave like a system generated by a sequence of independent coin tosses. The first class of smooth systems for which such phenomena where observed is that of the uniformly hyperbolic systems, or Anosov systems [⁠1⁠ D. V. Anosov, Roughness of geodesic flows on compact Riemannian manifolds of negative curvature. (in Russian) Dokl. Akad. Nauk SSSR 145, 707–709 (1962) ], i.e., systems for which the tangent space at every point splits into contracting and expanding directions for the derivative of the map $f$ and moreover these directions are invariant under $f$. This in particular implies that all Lyapunov exponents are non-zero.

2.1 Uniformly hyperbolic systems

The main class of uniformly hyperbolic examples is given by hyperbolic matrices with integer entries. Rather than giving a general definition of a uniformly hyperbolic system, we will focus on these examples which should provide some intuition for the general situation.

Readers not familiar with dynamical systems may restrict their attention to hyperbolic matrices in what follows. The main mechanism that allows to study chaotic properties of uniformly hyperbolic systems is the existence of so-called Markov partitions, constructed in [⁠5⁠ R. Bowen, Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92, 725–747 (1970) , ⁠57⁠ Ya. G. Sinaĭ, Markov partitions and C-diffeomorphisms. Funct. Anal. Appl. 2, 61–82 (1968) ]. They allow showing that a uniformly hyperbolic dynamical system is ‘almost’ Hölder conjugate to a subshift of finite type (SFT). SFTs are a class of symbolic systems which essentially exhibit the same statistical and chaotic properties as systems generated by sequences of independent coin tosses (Bernoulli shifts). Rather than defining Markov partitions in full generality, we will just present one simple example of a Markov partition for a non-invertible map. This should give the readers a general idea on usefulness of such partitions.

Unfortunately, the powerful tool of Markov partitions is usually not available for systems that are not hyperbolic, i.e., for partially hyperbolic systems, or, in particular, systems with some Lyapunov exponents equal to 0. This is a much wider class of systems for which there might be some directions in the tangent space which do not contract or expand (as fast) when iterated by the derivative. The simplest examples would be an integer matrix like in Example ⁠2.1⁠, but for which some of the eigenvalues have absolute value one. Another class of straightforward examples would be time-1 maps of Anosov flows (think about the geodesic flow on the unit tangent bundle of a hyperbolic surface). The flow direction is then an isometry. Statistical and chaotic properties of systems for which not all Lyapunov exponents are non-zero are much less understood. There are two main classes for which one usually applies completely different methods: (a) systems with positive entropy, or equivalently, with some of the Lyapunov exponents different from zero (i.e., there are some directions in which we see contraction or expansion); and (b) systems of zero entropy (with all Lyapunov exponents equal to zero). We will discuss these two classes in separate subsections.

2.2 Systems with positive entropy

As mentioned above, the general theory of systems with some Lyapunov exponents equal to zero is much less understood and there is no general framework to study chaotic properties in this class. In the last century, significant partial progress was made on understanding qualitative (ergodic) properties of such systems that we will now describe.

Qualitative properties

Qualitative properties can be defined for abstract measure-preserving systems. The strongest such property is being Bernoulli, i.e., being measure-theoretically isomorphic to a Bernoulli shift (a system generated by a sequence of independent coin tosses). A weaker property is called the $K$-property ($K$ for Kolmogorov) which is equivalent to saying that every factor of the system has positive entropy [⁠54⁠ V. A. Rokhlin and Ya. G. Sinaĭ, The structure and properties of invariant measurable partitions. (in Russian) Dokl. Akad. Nauk SSSR 141, 1038–1041 (1961) ]. Some weaker properties are mixing, weak mixing and ergodicity, but for simplicity we will focus here on the $K$ and Bernoulli properties only. Anatole Katok [⁠30⁠ A. Katok, Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110, 529–547 (1979) ], and then Brin, Feldman and Katok [⁠6⁠ M. I. Brin, J. Feldman and A. Katok, Bernoulli diffeomorphisms and group extensions of dynamical systems with non-zero characteristic exponents. Ann. of Math. (2) 113, 159–179 (1981) ], have shown that every smooth manifold of dimension at least 2 supports a Bernoulli diffeomorphisms, and so there are no topological restrictions for Bernoullicity in the smooth setting. The main development for establishing $K$ and Bernoulli properties was to use some geometric structures derived from the existence of non-zero exponents (stable and unstable manifolds). Sinai [⁠56⁠ Ya. G. Sinaĭ, On the concept of entropy for a dynamic system. Dokl. Akad. Nauk SSSR (in Russian) 124, 768–771 (1959) ] has shown that the $K$-property follows from ergodicity of the so-called unstable foliation. This is still the main mechanism for showing $K$-property for smooth dynamical systems, used widely in literature, see for example [⁠8⁠ K. Burns and A. Wilkinson, On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171, 451–489 (2010) ]. The theory of Bernoulli shifts was developed in the second half of the last century, culminating in Ornstein’s theory which allowed for their full classification in terms of entropy [⁠42⁠ D. Ornstein, Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4, 337–352 (1970) ]. In particular, the very weak Bernoulli property introduced in [⁠42⁠ D. Ornstein, Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4, 337–352 (1970) ] turned out to be a very useful tool in establishing Bernoullicity of smooth systems with (some) non-zero exponents. This came with the work of Ornstein and Weiss [⁠44⁠ D. S. Ornstein and B. Weiss, Geodesic flows are Bernoullian. Israel J. Math. 14, 184–198 (1973) ], where they used a geometric method to establish the very weak Bernoulli property for hyperbolic toral automorphisms, as well as for geodesic flows. Even though the systems they considered where algebraic, the introduced method proved to be applicable in a much more general setting. Specifically, the method is based on finding, for a given $N$, a matching between two pieces of typical unstable manifolds, i.e., a measure-preserving map ${\Theta }_N$ between these unstable manifolds such that the points $x$ and ${\Theta }_N(x)$ are close for most of the iterates under the dynamics when the iterates are taken from the set $[0,N]$. This mechanism is to this day the main technique to study the Bernoulli property for smooth systems and has been used in various settings, e.g., [⁠7⁠ L. A. Bunimovič, On a class of special flows. Math. USSR Izv. 8, 219–232 (1974) , ⁠10⁠ N. I. Chernov and C. Haskell, Nonuniformly hyperbolic K-systems are Bernoulli. Ergodic Theory Dynam. Systems 16, 19–44 (1996) , ⁠11⁠ S. G. Dani, Bernoullian translations and minimal horospheres on homogeneous spaces. J. Indian Math. Soc. (N.S.) 40, 245–284 (1976) (1976) , ⁠36⁠ F. Ledrappier, Some properties of absolutely continuous invariant measures on an interval. Ergodic Theory Dynam. Systems 1, 77–93 (1981) , ⁠46⁠ Ya. B. Pesin, Geodesic flows on closed Riemannian manifolds without focal points. Math. USSR Izv. 11, 1195–1228 (1977) , ⁠48⁠ M. Ratner, Anosov flows with Gibbs measures are also Bernoullian. Israel J. Math. 17, 380–391 (1974) , ⁠49⁠ M. Ratner, Bernoulli flow over maps of the interval. Israel J. Math. 31, 298–314 (1978) ]. Let us mention that despite considerable progress in the study of qualitative properties of smooth systems there are a number of open questions regarding whether a given dynamical system is Bernoulli or not. In particular, in [⁠16⁠ D. Dolgopyat, A. Kanigowski and F. Rodriguez Hertz, Exponential mixing implies Bernoulli. Ann. of Math. (2) 199, 1225–1292 (2024) ] the authors showed that a smooth diffeomorphism which is exponentially mixing, is in fact Bernoulli. The methods used in [⁠16⁠ D. Dolgopyat, A. Kanigowski and F. Rodriguez Hertz, Exponential mixing implies Bernoulli. Ann. of Math. (2) 199, 1225–1292 (2024) ] seem to suggest that there is a ‘competition’ between mixing rates of the system and growth on the center space which would determine if a system is Bernoulli or not. It is also not known if exponential mixing (for Hölder functions) implies Bernoulli in the non-smooth (e.g., symbolic) setting. Finally, let us mention that Kolmogorov initially conjectured that the $K$ and Bernoulli properties are equivalent. This was shown not to be the case by Ornstein [⁠43⁠ D. S. Ornstein, An example of a Kolmogorov automorphism that is not a Bernoulli shift. Adv. Math. 10, 49–62 (1973) ] in the abstract setting and independently by Katok [⁠31⁠ A. Katok, Smooth non-Bernoulli K-automorphisms. Invent. Math. 61, 291–299 (1980) ] and Rudolph [⁠55⁠ D. J. Rudolph, Asymptotically Brownian skew products give non-loosely Bernoulli K-automorphisms. Invent. Math. 91, 105–128 (1988) ] in the smooth setting. In [⁠29⁠ A. Kanigowski, F. Rodriguez Hertz and K. Vinhage, On the non-equivalence of the Bernoulli and K properties in dimension four. J. Mod. Dyn. 13, 221–250 (2018) ] the authors showed that $K$ does not imply Bernoulli in dimension 4. It is known that it does in dimension 2 [⁠45⁠ Ya. B. Pesin, Characteristic Lyapunov exponents and smooth ergodic theory. Russian Math. Surveys 32, 55–114 (1977) ]. The problem in dimension 3 is one of the big open questions in the field [⁠32⁠ A. Katok, Five most resistant problems in dynamics. MSRI-Evans Lecture, Berkeley (2004) ].

Quantitative properties

Quantitative properties are those which use the fact that the system is a smooth diffeomorphism acting on a smooth manifold. Main quantitative properties are quantitative mixing (or decay of correlations), central limit theorem (CLT), large deviations, quantitative ergodicity. Quantitative properties are much less understood than qualitative ones. There are still open questions regarding interplay of quantitative and qualitative properties. In what follows we will mostly focus on quantitative mixing and central limit theorem. In fact, if the system has fast decay of correlations of all orders, then a CLT follows, see, e.g., [⁠4⁠ M. Björklund and A. Gorodnik, Central limit theorems for group actions which are exponentially mixing of all orders. J. Anal. Math. 141, 457–482 (2020) ]. The problem of establishing quantitative mixing rates for a given smooth system is difficult and widely open in general, even though a lot of progress was made for algebraic systems where one uses representation theory, see, e.g., [⁠25⁠ R. Howe, On a notion of rank for unitary representations of the classical groups. In Harmonic analysis and group representations, Liguori, Naples, 223–331 (1982) , ⁠34⁠ D. Y. Kleinbock and G. A. Margulis, Bounded orbits of nonquasiunipotent flows on homogeneous spaces. In Sinaĭ’s Moscow Seminar on Dynamical Systems, Amer. Math. Soc. Transl. Ser. 2 171, Amer. Math. Soc., Providence, RI, 141–172 (1996) , ⁠40⁠ C. C. Moore, Exponential decay of correlation coefficients for geodesic flows. In Group representations, ergodic theory, operator algebras, and mathematical physics (Berkeley, Calif., 1984), Math. Sci. Res. Inst. Publ. 6, Springer, New York, 163–181 (1987) ]. The most successful methods of establishing (exponential) rates of mixing is by using transfer operators and their spectral gaps, initiated in the fundamental work of Dmitry Dolgopyat [⁠13⁠ D. Dolgopyat, On decay of correlations in Anosov flows. Ann. of Math. (2) 147, 357–390 (1998) ]. In fact, it seems that this method (or variants thereof) is the only approach for establishing rates of mixing in the smooth setting. It has been used by many authors in various situations, see, e.g., [⁠37⁠ C. Liverani, On contact Anosov flows. Ann. of Math. (2) 159, 1275–1312 (2004) , ⁠60⁠ M. Tsujii and Z. Zhang, Smooth mixing Anosov flows in dimension three are exponentially mixing. Ann. of Math. (2) 197, 65–158 (2023) ] and references therein. In fact, this method also allows one to get other statistical properties, such as large deviations and CLT. It is based on translating the problem on (exponential) mixing into a problem concerning the spectral nature of a naturally associated operator (the transfer operator). One can then use tools from complex and harmonic analysis to study the spectrum of the system on so-called anisotropic Banach spaces, see, e.g., the survey [⁠12⁠ M. F. Demers, A gentle introduction to anisotropic Banach spaces. Chaos Solitons Fractals 116, 29–42 (2018) ] and references therein. As mentioned, existence of a spectral gap usually implies all statistical properties, and so if one wants systems with exotic behavior (enjoying some, but not all of the properties) one needs to introduce different methods. In particular, it is not known if there exists a smooth dynamical system which is exponentially mixing, but not exponentially mixing of order 3. In [⁠14⁠ D. Dolgopyat, C. Dong, A. Kanigowski and P. Nándori, Flexibility of statistical properties for smooth systems satisfying the central limit theorem. Invent. Math. 230, 31–120 (2022) ] the authors have produced exotic examples of smooth dynamical systems (with finite smoothness) which have zero entropy and still satisfy the CLT. A $C^{\infty }$ flow of zero entropy and with CLT was constructed in [⁠15⁠ D. Dolgopyat, B. Fayad and A. Kanigowski, Smooth zero entropy flows satisfying the classical central limit theorem. J. Éc. polytech. Math. 12, 1–22 (2025) ]. Existence of a $C^{\infty }$ map with zero entropy and with a CLT is still an open question. As mentioned in the previous section, it is known that every manifold of dimension at least 2 supports a Bernoulli diffeomorphism. It is not known if every manifold of dimension at least 2 supports a smooth diffeomorphism which satisfies a CLT as well as a smooth diffeomorphism which is exponentially mixing.

2.3 Systems with zero entropy

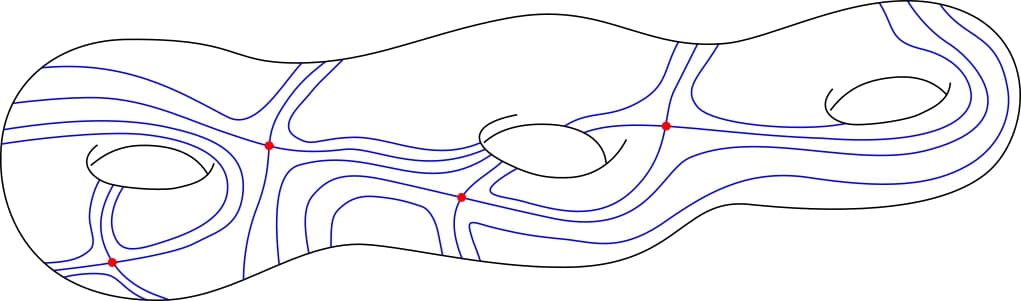
The world of zero-entropy systems in general is too wide to have any meaningful general structures. According to, e.g. [⁠33⁠ A. Katok and B. Hasselblatt, Introduction to the modern theory of dynamical systems. Encyclopedia Math. Appl., Cambridge University Press (1995) ], there are two rather different main classes of zero-entropy systems, elliptic systems and parabolic systems. The main model for elliptic systems is provided by irrational rotations on compact Abelian groups (irrational rotations of the circle being the main example), but there are also less rigid examples of elliptic dynamics [⁠20⁠ B. Fayad and A. Katok, Constructions in elliptic dynamics. Ergodic Theory Dynam. Systems 24, 1477–1520 (2004) ]. Elliptic dynamics is usually characterized by a rather non-chaotic, tame behavior where mixing is often precluded. We will focus on the class of parabolic systems and briefly highlight typical chaotic features in this class. Unlike the hyperbolic world, there is no strict definition of a parabolic system. It is rather a set of common characteristics that is an indicator of parabolic behavior. The prime class of parabolic systems are horocycle flows. In algebraic language, the horocycle flow $(h_t)$ is given by the action of the matrix $(\begin{array}{cc}1& t\\ 0& 1\end{array})$ acting on finite-volume quotients of the group $SL(2,\mathbb{R})$. Ergodic and statistical features of horocycle flows are the model behavior in the class of parabolic systems. More generally, unipotent flows on quotients of semisimple Lie group constitute a wider class of (algebraic) parabolic systems. Yet another class of (non-algebraic) systems that can be classified as parabolic (even though they also exhibit some elliptic-like behavior) is the class of smooth flows on surfaces, known as locally Hamiltonian flows (see Figure ⁠2⁠).

This is the class in which recently many tools from homogeneous dynamics were adapted to the non-algebraic setting. There are also systems which share both elliptic and parabolic characteristics: interval exchange transformations and translation flows, nilrotations on nilmanifolds, reparametrizations (or perturbations) of all the above-mentioned examples. One of the typical features of parabolic systems is that the orbit growth (or orbit divergence) happens typically at polynomial (or logarithmic) rate. This is the difference with hyperbolic systems, where the growth is exponential, and also with elliptic systems, where the growth is often sub-logarithmic. Moreover, typically the divergence of all nearby conditions occurs along well-understood, structured directions. Some characteristic features that one usually observes for parabolic systems are: small set of invariant measures (often a unique such measure), polynomial (or logarithmic) rates of mixing, which are usually obtained by the mixing via shearing mechanism, polynomial deviation of ergodic averages, absolutely continuous or Lebesgue spectrum, variants of Ratner’s property (shearing in the direction of the dynamics), structured sets of joinings, ‘nice’ orbit closures. These properties for horocycle flows (or more generally unipotent flows) were established by a number of authors: Marina Ratner in her seminal work [⁠50⁠ M. Ratner, Horocycle flows, joinings and rigidity of products. Ann. of Math. (2) 118, 277–313 (1983) , ⁠52⁠ M. Ratner, On measure rigidity of unipotent subgroups of semisimple groups. Acta Math. 165, 229–309 (1990) ] studied orbit closures and measure rigidity for unipotent flows, in [⁠51⁠ M. Ratner, The rate of mixing for geodesic and horocycle flows. Ergodic Theory Dynam. Systems 7, 267–288 (1987) ] Ratner also studied rates of mixing for horocycle flows. Higher-order mixing was established by Marcus [⁠39⁠ B. Marcus, Ergodic properties of horocycle flows for surfaces of negative curvature. Ann. of Math. (2) 105, 81–105 (1977) ]. Deviation of ergodic averages was studied in [⁠21⁠ L. Flaminio and G. Forni, Invariant distributions and time averages for horocycle flows. Duke Math. J. 119, 465–526 (2003) ] and [⁠59⁠ A. Strömbergsson, On the deviation of ergodic averages for horocycle flows. J. Mod. Dyn. 7, 291–328 (2013) ].

Much less was known until recently for parabolic systems that are not algebraic. This has changed significantly in the last 20 years, in which major progress in the study of spectral, mixing and rigidity properties of these systems was made. Due to limited space we will again only provide a list of references on the topic: deviation of ergodic averages was studied in [⁠22⁠ G. Forni, Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. of Math. (2) 155, 1–103 (2002) , ⁠23⁠ K. Frączek and M. Kim, New phenomena in deviation of Birkhoff integrals for locally Hamiltonian flows. J. Reine Angew. Math. 807, 81–149 (2024) , ⁠24⁠ K. Frączek and C. Ulcigrai, On the asymptotic growth of Birkhoff integrals for locally Hamiltonian flows and ergodicity of their extensions. Comment. Math. Helv. 99, 231–354 (2024) ]. Mixing properties were established in [⁠17⁠ B. Fayad, Polynomial decay of correlations for a class of smooth flows on the two torus. Bull. Soc. Math. France 129, 487–503 (2001) , ⁠53⁠ D. Ravotti, Quantitative mixing for locally Hamiltonian flows with saddle loops on compact surfaces. Ann. Henri Poincaré 18, 3815–3861 (2017) , ⁠58⁠ Y. G. Sinaĭ and K. M. Khanin, Mixing for some classes of special flows over rotations of the circle. Funct. Anal. Appl. 26, 155–169 (1992) , ⁠61⁠ C. Ulcigrai, Mixing of asymmetric logarithmic suspension flows over interval exchange transformations. Ergodic Theory Dynam. Systems 27, 991–1035 (2007) , ⁠62⁠ C. Ulcigrai, Absence of mixing in area-preserving flows on surfaces. Ann. of Math. (2) 173, 1743–1778 (2011) ]. Higher-order mixing was studied in [⁠19⁠ B. Fayad and A. Kanigowski, Multiple mixing for a class of conservative surface flows. Invent. Math. 203, 555–614 (2016) , ⁠26⁠ A. Kanigowski, J. Kułaga-Przymus and C. Ulcigrai, Multiple mixing and parabolic divergence in smooth area-preserving flows on higher genus surfaces. J. Eur. Math. Soc. (JEMS) 21, 3797–3855 (2019) , ⁠28⁠ A. Kanigowski and D. Ravotti, Multiple mixing for parabolicsystems. arXiv:2410.13686v1 (2024) ]. Joinings and rigidity were studied in [⁠2⁠ P. Berk and A. Kanigowski, Spectral disjointness of rescalings of some surface flows. J. Lond. Math. Soc. (2) 103, 901–942 (2021) , ⁠27⁠ A. Kanigowski, M. Lemańczyk and C. Ulcigrai, On disjointness properties of some parabolic flows. Invent. Math. 221, 1–111 (2020) ]. Spectral properties were studied in [⁠9⁠ J. Chaika, K. Frączek, A. Kanigowski and C. Ulcigrai, Singularity of the spectrum for smooth area-preserving flows in genus two and translation surfaces well approximated by cylinders. Comm. Math. Phys. 381, 1369–1407 (2021) , ⁠18⁠ B. Fayad, G. Forni and A. Kanigowski, Lebesgue spectrum of countable multiplicity for conservative flows on the torus. J. Amer. Math. Soc. 34, 747–813 (2021) ].

Even though there has been significant progress on general parabolic systems, there are still many directions which are quite open: spectral features (the spectral type and the multiplicity function) of non-algebraic parabolic systems are still not known in many cases. Optimal rates of mixing and higher-order mixing is another open problem in the area. And despite some partial results, the theory of joinings is another problem that is rather widely open.

Adam Kanigowski is a professor at the University of Maryland (USA) and at Jagiellonian University (Poland). He obtained his PhD in 2015 at the Institute of Mathematics in Warsaw. His research is in ergodic theory and in dynamical systems, more precisely he studies statistical properties of smooth systems on manifolds and interactions of dynamical systems and number theory. Beyond mathematics, he likes participating in long-distance triathlons (Ironmans). akanigow@umd.edu

1. ¹

   Taken from https://commons.wikimedia.org/wiki/File:Lorenz_system_r28_s10_b2-6666.png.

2. ²

   See https://galileo-unbound.blog/2019/06/16/vladimir-arnolds-cat-map/.

References

1. D. V. Anosov, Roughness of geodesic flows on compact Riemannian manifolds of negative curvature. (in Russian) Dokl. Akad. Nauk SSSR 145, 707–709 (1962)
2. P. Berk and A. Kanigowski, Spectral disjointness of rescalings of some surface flows. J. Lond. Math. Soc. (2) 103, 901–942 (2021)
3. G. D. Birkhoff, Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA 17, 656–660 (1931)
4. M. Björklund and A. Gorodnik, Central limit theorems for group actions which are exponentially mixing of all orders. J. Anal. Math. 141, 457–482 (2020)
5. R. Bowen, Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92, 725–747 (1970)
6. M. I. Brin, J. Feldman and A. Katok, Bernoulli diffeomorphisms and group extensions of dynamical systems with non-zero characteristic exponents. Ann. of Math. (2) 113, 159–179 (1981)
7. L. A. Bunimovič, On a class of special flows. Math. USSR Izv. 8, 219–232 (1974)
8. K. Burns and A. Wilkinson, On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171, 451–489 (2010)
9. J. Chaika, K. Frączek, A. Kanigowski and C. Ulcigrai, Singularity of the spectrum for smooth area-preserving flows in genus two and translation surfaces well approximated by cylinders. Comm. Math. Phys. 381, 1369–1407 (2021)
10. N. I. Chernov and C. Haskell, Nonuniformly hyperbolic K-systems are Bernoulli. Ergodic Theory Dynam. Systems 16, 19–44 (1996)
11. S. G. Dani, Bernoullian translations and minimal horospheres on homogeneous spaces. J. Indian Math. Soc. (N.S.) 40, 245–284 (1976) (1976)
12. M. F. Demers, A gentle introduction to anisotropic Banach spaces. Chaos Solitons Fractals 116, 29–42 (2018)
13. D. Dolgopyat, On decay of correlations in Anosov flows. Ann. of Math. (2) 147, 357–390 (1998)
14. D. Dolgopyat, C. Dong, A. Kanigowski and P. Nándori, Flexibility of statistical properties for smooth systems satisfying the central limit theorem. Invent. Math. 230, 31–120 (2022)
15. D. Dolgopyat, B. Fayad and A. Kanigowski, Smooth zero entropy flows satisfying the classical central limit theorem. J. Éc. polytech. Math. 12, 1–22 (2025)
16. D. Dolgopyat, A. Kanigowski and F. Rodriguez Hertz, Exponential mixing implies Bernoulli. Ann. of Math. (2) 199, 1225–1292 (2024)
17. B. Fayad, Polynomial decay of correlations for a class of smooth flows on the two torus. Bull. Soc. Math. France 129, 487–503 (2001)
18. B. Fayad, G. Forni and A. Kanigowski, Lebesgue spectrum of countable multiplicity for conservative flows on the torus. J. Amer. Math. Soc. 34, 747–813 (2021)
19. B. Fayad and A. Kanigowski, Multiple mixing for a class of conservative surface flows. Invent. Math. 203, 555–614 (2016)
20. B. Fayad and A. Katok, Constructions in elliptic dynamics. Ergodic Theory Dynam. Systems 24, 1477–1520 (2004)
21. L. Flaminio and G. Forni, Invariant distributions and time averages for horocycle flows. Duke Math. J. 119, 465–526 (2003)
22. G. Forni, Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. of Math. (2) 155, 1–103 (2002)
23. K. Frączek and M. Kim, New phenomena in deviation of Birkhoff integrals for locally Hamiltonian flows. J. Reine Angew. Math. 807, 81–149 (2024)
24. K. Frączek and C. Ulcigrai, On the asymptotic growth of Birkhoff integrals for locally Hamiltonian flows and ergodicity of their extensions. Comment. Math. Helv. 99, 231–354 (2024)
25. R. Howe, On a notion of rank for unitary representations of the classical groups. In Harmonic analysis and group representations, Liguori, Naples, 223–331 (1982)
26. A. Kanigowski, J. Kułaga-Przymus and C. Ulcigrai, Multiple mixing and parabolic divergence in smooth area-preserving flows on higher genus surfaces. J. Eur. Math. Soc. (JEMS) 21, 3797–3855 (2019)
27. A. Kanigowski, M. Lemańczyk and C. Ulcigrai, On disjointness properties of some parabolic flows. Invent. Math. 221, 1–111 (2020)
28. A. Kanigowski and D. Ravotti, Multiple mixing for parabolicsystems. arXiv:2410.13686v1 (2024)
29. A. Kanigowski, F. Rodriguez Hertz and K. Vinhage, On the non-equivalence of the Bernoulli and K properties in dimension four. J. Mod. Dyn. 13, 221–250 (2018)
30. A. Katok, Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110, 529–547 (1979)
31. A. Katok, Smooth non-Bernoulli K-automorphisms. Invent. Math. 61, 291–299 (1980)
32. A. Katok, Five most resistant problems in dynamics. MSRI-Evans Lecture, Berkeley (2004)
33. A. Katok and B. Hasselblatt, Introduction to the modern theory of dynamical systems. Encyclopedia Math. Appl., Cambridge University Press (1995)
34. D. Y. Kleinbock and G. A. Margulis, Bounded orbits of nonquasiunipotent flows on homogeneous spaces. In Sinaĭ’s Moscow Seminar on Dynamical Systems, Amer. Math. Soc. Transl. Ser. 2 171, Amer. Math. Soc., Providence, RI, 141–172 (1996)
35. A. N. Kolmogorov, A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. (in Russian) Dokl. Akad. Nauk SSSR (N.S.) 119, 861–864 (1958)
36. F. Ledrappier, Some properties of absolutely continuous invariant measures on an interval. Ergodic Theory Dynam. Systems 1, 77–93 (1981)
37. C. Liverani, On contact Anosov flows. Ann. of Math. (2) 159, 1275–1312 (2004)
38. E. N. Lorenz, Deterministic nonperiodic flow. J. Atmospheric Sci. 20, 130–141 (1963)
39. B. Marcus, Ergodic properties of horocycle flows for surfaces of negative curvature. Ann. of Math. (2) 105, 81–105 (1977)
40. C. C. Moore, Exponential decay of correlation coefficients for geodesic flows. In Group representations, ergodic theory, operator algebras, and mathematical physics (Berkeley, Calif., 1984), Math. Sci. Res. Inst. Publ. 6, Springer, New York, 163–181 (1987)
41. J. von Neumann, Proof of the quasi-ergodic hypothesis. Proc. Natl. Acad. Sci. USA 18, 70–82 (1932)
42. D. Ornstein, Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4, 337–352 (1970)
43. D. S. Ornstein, An example of a Kolmogorov automorphism that is not a Bernoulli shift. Adv. Math. 10, 49–62 (1973)
44. D. S. Ornstein and B. Weiss, Geodesic flows are Bernoullian. Israel J. Math. 14, 184–198 (1973)
45. Ya. B. Pesin, Characteristic Lyapunov exponents and smooth ergodic theory. Russian Math. Surveys 32, 55–114 (1977)
46. Ya. B. Pesin, Geodesic flows on closed Riemannian manifolds without focal points. Math. USSR Izv. 11, 1195–1228 (1977)
47. H. Poincaré, Sur le problème des trois corps et les équations de la dynamique. Acta Math. 13, 1–270 (1890)
48. M. Ratner, Anosov flows with Gibbs measures are also Bernoullian. Israel J. Math. 17, 380–391 (1974)
49. M. Ratner, Bernoulli flow over maps of the interval. Israel J. Math. 31, 298–314 (1978)
50. M. Ratner, Horocycle flows, joinings and rigidity of products. Ann. of Math. (2) 118, 277–313 (1983)
51. M. Ratner, The rate of mixing for geodesic and horocycle flows. Ergodic Theory Dynam. Systems 7, 267–288 (1987)
52. M. Ratner, On measure rigidity of unipotent subgroups of semisimple groups. Acta Math. 165, 229–309 (1990)
53. D. Ravotti, Quantitative mixing for locally Hamiltonian flows with saddle loops on compact surfaces. Ann. Henri Poincaré 18, 3815–3861 (2017)
54. V. A. Rokhlin and Ya. G. Sinaĭ, The structure and properties of invariant measurable partitions. (in Russian) Dokl. Akad. Nauk SSSR 141, 1038–1041 (1961)
55. D. J. Rudolph, Asymptotically Brownian skew products give non-loosely Bernoulli K-automorphisms. Invent. Math. 91, 105–128 (1988)
56. Ya. G. Sinaĭ, On the concept of entropy for a dynamic system. Dokl. Akad. Nauk SSSR (in Russian) 124, 768–771 (1959)
57. Ya. G. Sinaĭ, Markov partitions and C-diffeomorphisms. Funct. Anal. Appl. 2, 61–82 (1968)
58. Y. G. Sinaĭ and K. M. Khanin, Mixing for some classes of special flows over rotations of the circle. Funct. Anal. Appl. 26, 155–169 (1992)
59. A. Strömbergsson, On the deviation of ergodic averages for horocycle flows. J. Mod. Dyn. 7, 291–328 (2013)
60. M. Tsujii and Z. Zhang, Smooth mixing Anosov flows in dimension three are exponentially mixing. Ann. of Math. (2) 197, 65–158 (2023)
61. C. Ulcigrai, Mixing of asymmetric logarithmic suspension flows over interval exchange transformations. Ergodic Theory Dynam. Systems 27, 991–1035 (2007)
62. C. Ulcigrai, Absence of mixing in area-preserving flows on surfaces. Ann. of Math. (2) 173, 1743–1778 (2011)