Please do touch: maths you cannot resist grabbing

The EMS Simon Norton Prize for Mathematics Outreach (Katie Chicot)

The EMS Outreach and Public Engagement Committee is focussing on:

1. Building a community of those who are involved in maths engagement.

2. Raising the profile and status of maths engagement work.

3. Sharing good practice in outreach, evaluation and fundraising.

The committee decided to establish an international prize, the EMS Simon Norton Prize for Mathematics Outreach, to achieve all of the above. The prize will be awarded every two years and is supported by a private donor for 2024, 2026 and 2028. Earlier this year we received 33 excellent entries from around the world for 2024. The judging panel consisted of members of the committee and the former chair of the committee, Roberto Natalini.

Nina Gasking from Maison des mathématiques et de l’informatique (MMI) in Lyon was awarded first place at the Matrix $\times$ Imaginary conference this summer. The panel were impressed with the originality, reach, and mathematical depth of this project, which you can read about in this article. In addition to this, several of the entries are displayed on the committee’s webpage to demonstrate best practice in mathematics outreach.⁠¹⁠https://euromathsoc.org/committee-outreach-Simon-Norton-Prize-2024

Please do touch: maths you cannot resist grabbing (Nina Gasking)

Mathematical outreach, much like mathematics itself, is hard to define. Most people will agree that it refers to efforts made to communicate and promote the understanding and appreciation of mathematics to a broader audience, often outside the formal academic setting. The goal is to break down the idea that mathematics is difficult or inaccessible and instead foster curiosity, engagement, and appreciation for its beauty and utility. But how can we accomplish this? There are many ways to do outreach, and I would like to share mine.

MMI: The home of hands-on maths

I cannot explain my work without first talking about where I do it: the Maison des mathématiques et de l’informatique⁠²⁠Translated to: Home of Mathematics and Computer Science. (MMI) in Lyon, France.⁠³⁠https://mmi-lyon.fr Founded in 2012 as part of LabEx MILYON – which brings together the scientific community in mathematics and computer science in Lyon – the MMI is a centre dedicated to outreach. We offer a wide range of activities, from exhibitions and workshops to theatre performances and conferences. During the 2023–2024 school year alone, we welcomed 450 school groups, and in total, we reached about 4,000 visitors from the general public.

Our values are at the core of everything we do: inclusivity (so that everyone feels at home), hands-on activities, and a focus on “human outreach.” By human outreach, I mean that whenever you visit the MMI, there is always someone there to engage with you personally. Whether it is a guided tour of our exhibitions or a workshop session, we ensure a human touch – someone to answer questions, offer support, or prompt deeper reflection. This interaction makes people feel involved and valued.

To explain what we do, I would like to share a specific example. Earlier this year, I had the honour of receiving the EMS Simon Norton Prize for Mathematics Outreach for an exhibition we developed called “Dans ma cuisine” (“In My Kitchen”). I will use this as my example. While I curated the exhibition, the project was a team effort, with many dedicated contributors.

A quick walkthrough of the exhibition

Of course, you are more than welcome to visit Lyon and experience the exhibition in person (it will be running until June 2025). However, for those who cannot make it, here is a glimpse of what you can expect to find.

When most people think of maths in the context of cooking, they often think of proportionality. Well… we did not even mention it in the exhibition! From the start, it was clear we did not want to focus on a single mathematical concept. Instead, we wanted to use the kitchen as a pretext to explore different mathematical and computer science topics. The whole exhibition was structured around having hands-on activities, so the public could engage directly with the maths. We also wanted to encourage reasoning and problem-solving skills, pushing our audience to discover mathematical thinking more than learning about specific topics.

With these goals in mind, the structure of the exhibition began to take shape. We created four thematic spaces, with a total of eleven stands. Each stand tackles a specific scientific theme, paired with an interactive activity. The kitchen serves as the cohesive element, tying everything together. Since there was no common scientific thread, we came up with the idea of introducing a fictional character – someone passionate about maths, computer science, and cooking. This character guides visitors through different stages of the cooking process, which form the four spaces in the exhibition: Preparing, Cooking, Sharing, and Chatting.

Here is a taste of the scientific topics covered:

• Preparing (as in planning your recipe or menu, or thinking about who you will invite): Algorithms, data organisation, and scheduling.

• Cooking (self-explanatory): Entropy, harmonic functions, packing problems, and side-channel attacks.

• Sharing (your pizza is ready, and now it is time to divide it among your guests): Probability and statistics, two-player games, and the necklace splitting problem.

• Chatting (you’ve finished eating, and now it is time for conversation over tea or coffee): Meet actual researchers!

A closer look at one activity

Hopefully, the list of topics has piqued your curiosity about what is inside the exhibition. While I cannot dive into every idea here, I will explain one particular activity.

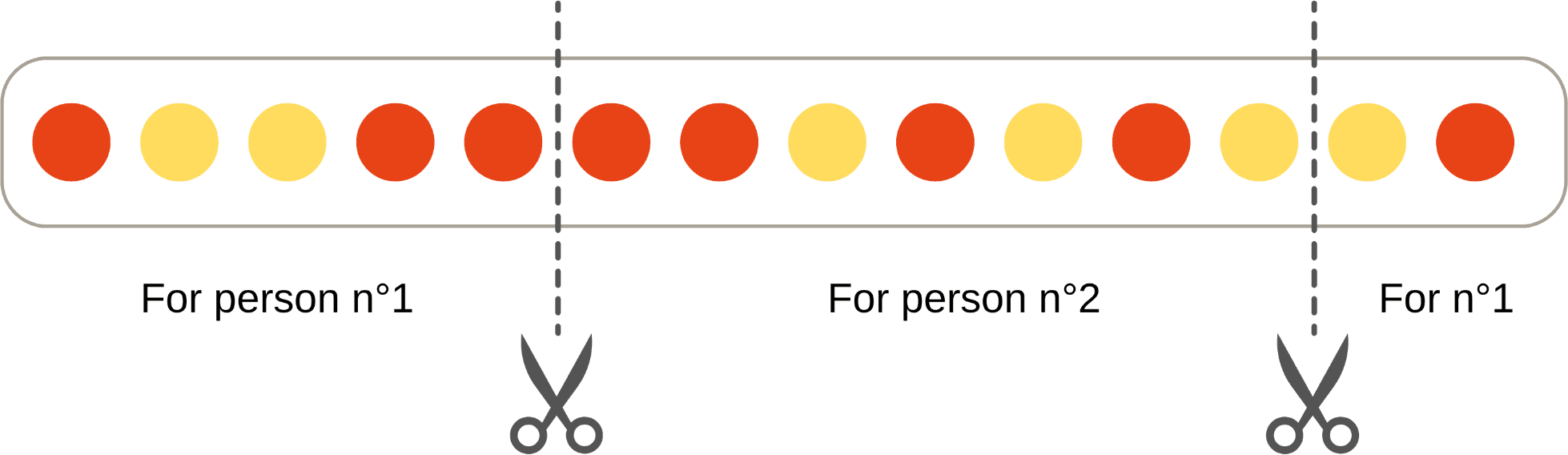
Here is the activity: two people want to share a cake evenly, including the decorations on top. The cake has 8 red and 6 yellow decorations, meaning each person should get 4 red and 3 yellow pieces. They also want to achieve this with the fewest number of cuts.

This solution might seem obvious to you, but the beads (representing the decorations) can be rearranged. With a different configuration, the questions start piling up: Can you find a solution? Is there only one? Is there even a solution at all? Can you guarantee the minimum number of cuts? How would you prove it? These are some of the questions we ask visitors to consider. There are also two more cakes: one with three colours and another with four but in these cases, the beads cannot be moved. The task remains the same: share the cake evenly between two people with the fewest possible cuts. I will leave that challenge with you!

Now, why and how did I come up with this idea?

It all started with an idea of a mathematical topic: the necklace splitting problem. As we explored many scientific topics for the exhibition, this one stood out. Without going into all the technical details, here is why:

• It is a discrete problem: at the MMI we love to have hands-on activities without electronics or screens.

• The instructions are simple.

• With two colours, the proof uses the intermediate value theorem (easily explained with the cake). However, for three or more you need the Borsuk–Ulam theorem – a concept that, understandably, we rarely mention to visitors.

Once we had the concept, we focused on what we wanted people to take away from the activity. It was not about learning the necklace problem per se (we do not even mention its name in the exhibition). Instead, it was about helping visitors understand the difference between finding a solution and proving that it is the best possible one – proving that no fewer cuts can be made.

From there, we spent a lot of time designing the hands-on experience and carefully selecting instances for three and four colours. We had to find examples where intuitive algorithms did not work (as they do not in the general case) and where visitors could easily prove, without invoking the Borsuk–Ulam theorem, that no better solution was possible.

Engaging every visitor

Each stand in the exhibition is designed to be approachable at different levels, and the one I just described is no exception. Here are the layers of interaction:

1. Playing and finding a solution: anyone can try to find a solution by simply reading the instructions.

2. Proving optimality: the instructions mention cutting as little as possible, but visitors often need a little guidance to begin proving they’ve found the best solution. That is why someone from the MMI is always on hand during visits.

3. Generalising: If someone becomes deeply engaged with finding and proving the solutions, we might challenge them to think about what happens with n colours. This does not happen often, and that is fine!

These layers of engagement are possible because of the activity’s design and how it avoids overly technical terms. Whether visitors engage only at level 1 or go deeper, they never feel like they are missing out – something crucial for students who may not enjoy maths. They will appreciate that there is no “complicated formula” and that they can take away as much as they want from the activity, at their own pace.

You might notice that reading is not mentioned much, and that is deliberate. In this exhibition, reading is not fundamental. Each stand includes a panel that offers more insight into the science behind the activity, but these panels are meant as extras – they are not central to the experience. It is perfectly fine if someone visits the exhibition and does not read even a single one.

A slice of curiosity to go

This exhibition, like everything we do at the MMI, was the result of collaboration between many skilled people – researchers, outreach professionals, designers, and scenographers. It is a blend of ideas and expertise that, I hope, reflects my approach to outreach: making maths accessible, engaging, and hands-on. Through activities like these, we aim to spark curiosity, showing that maths is not just about solving problems, but also about discovering new ways to think.

So, if you ever feel hungry for a taste of mathematics, you know where to find us. But fair warning: you may leave with more questions than answers – and that is exactly how we like it!

Nina Gasking is a scientific outreach officer at the Maison des mathématiques et de l’informatique in Lyon since 2021. She has a master’s degree in pure mathematics from the University of Bordeaux and a master’s degree in scientific outreach from the Bordeaux Montaigne University. She is the exhibition curator of “Dans ma cuisine.” nina.gasking@ens-lyon.fr Katie Chicot is the CEO of MathsWorldUK, whose aim is to create the UK’s first Mathematics Discovery Centre. Alongside this Katie is a senior lecturer, staff tutor in mathematics and statistics at The Open University. This involves working with students and tutors, and creating materials. Both roles involve mathematics outreach and Katie is now the chair of the EMS Mathematics Outreach and Engagement Committee. katie.chicot@open.ac.uk

1. ¹

   https://euromathsoc.org/committee-outreach-Simon-Norton-Prize-2024

2. ²

   Translated to: Home of Mathematics and Computer Science.

3. ³

   https://mmi-lyon.fr