Having the right intuition and working hard is common to both the arts and the sciences. The high abstraction levels of mathematics, especially, seem to require an extra amount of intuitive guidance.
Listen2Intuition is a Mathematics & Arts exhibition project, which bridges disciplines by associative thinking, and aims to promote multidisciplinarity on an eye-to-eye level. For several years two mathematicians and an artist “listen” to each other across disciplines, generating artworks, compositions as well as new mathematical research.
1 Introduction: Mathematics & Arts
The story of Listen2Intuition originates in 2014 with a call for unconventional research by the University of Graz. The authors together with Gerhard Eckel from the University of Music and Performing Arts Graz were successful in a highly competitive two-stage selection procedure to ensure funding for the project Mathematics & Arts: Towards a balance between artistic intuition and mathematical complexity.
Mathematics and arts are linked throughout the development of the human civilisation: The Vedic scriptures, the Greek philosophers, the Renaissance with da Vinci’s universality and Palladio’s architecture, to mention just a few, are cornerstones of modern cultures. The twentieth century has seen an increasing influence of mathematical structures and the tools of dynamical systems on the arts.
For instance, the architect Le Corbusier developed the Modulor, a sequential system of scales constructed from the golden ratio and human body proportions, to design his outstanding buildings. The composer Iannis Xenakis (in his early years a co-worker of Le Corbusier) transferred the interest in mathematical and graphical structures to the field of music [10 I. Xenakis, Formalized music: Thought and mathematics in composition, Pendragon Press, NY (2001) ]. György Ligeti used a more metaphorical, transformative approach of scientific research in his concept of musical “permeability,” according to which a musical structure is “permeable” if it allows a free choice of intervals. And the designs of contemporary architects like Zaha Hadid rely in fundamental manner on the capacities of current 3D design software and fabrication techniques, and thus on a wide spectrum of geometrical and numerical routines.
Already these few examples suggest that whenever mathematics is instrumental in a creative process, a crucial component is the individual intuitive understanding of the artist: Le Corbusier wrote full of inspiration about his Modulor and left a legacy of outstanding buildings, such as the Unité d’Habitation in Marseille, yet he seemed not to have convinced a great many other architects to follow his path: Was it Le Corbusier’s talent to make the connection successful in practice?
1.1 Towards a balance between artistic intuition and mathematical complexity
Based on such thoughts, our project Mathematics & Arts: Towards a balance between artistic intuition and mathematical complexity set the agenda to research and explore mathematical structures and dynamical systems and to explore intuitive interfaces for non-mathematicians. The aim is to initiate an eye-to-eye dialogue across disciplines, be it between maths and arts or, say, between algebra and PDEs.
Here is an example of a project Originating from current algebraic research in representation theory, Figure 1 plots triangulations of an annulus connecting a given set of corner points on the inner and outer circles. From a mathematical point of view, the three left triangulations are topologically equivalent. The fourth is a borderline case featuring touching edges. The right-most instance exhibits intersecting edges, and so is no longer a triangulation from a mathematical perspective.
Instances of topological triangulations and beyond.
🅭🅯 CC BY 4.0However, Figure 1 was not created by a mathematician, but by the artist in the team. After having discussed the basic principles of triangulations and their relevance for current research on cluster algebras, Figure 1 is part of an approbation process guided by years of artistic training. The five instances in Figure 1 represent an aesthetic evolution, which is not afraid of breaking the mathematical rules of triangulations. Instead, there is an aesthetic continuity to the five images.
Figure 1 is intended to serve as an example that it is not necessary (and practically also not possible) for an artist to understand a comprehensive background of mathematical structures. What is necessary in initiating an interdisciplinary process is to identify representative aspects, which serve as points of inspiration. In the above example, two aspects were found the most important: First, the geometric possibilities themselves, and second, the topological properties, in particular the flexibility in the shape of edges, which constitutes a metaphor for the elasticity of borders in future artworks.
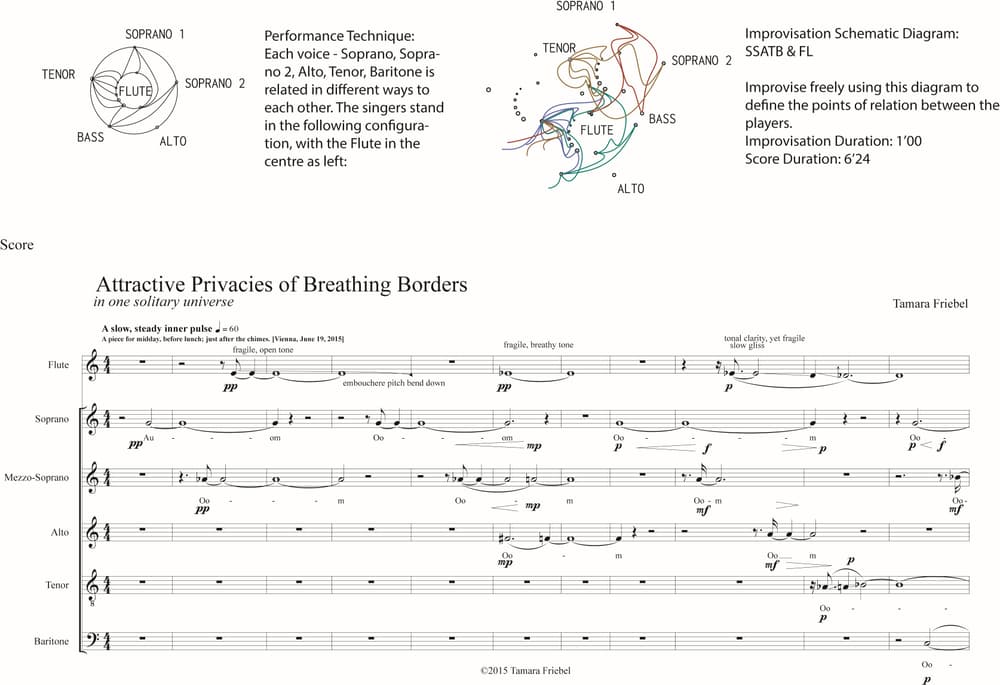
Attractive Privacies of Breathing Borders, in one solitary universe.
🅭🅯 CC BY 4.0In the interdisciplinary process of our project, we found it crucial for the artist to decide which aspects play a key role. The decision was made after listening to the explanations of the mathematical background, despite not understanding everything. After having listened, an intuitive assimilation process could start, which allows the participants to transform elements from foreign disciplines into something new within their own discipline. Here, Tamara Friebel continued to explore the geometric repertoire originating from Figure 1, derived from it a graphical concept of the composition Attractive Privacies of Breathing Borders before finally producing a score, see Figure 2 and below in Section 3.
2 The set-up of the exhibition project Listen2Intuition
During the work on the project Mathematics & Arts: Towards a balance between artistic intuition and mathematical complexity, the question of how to communicate with wider audiences became increasingly important. When talking to friends and colleagues, we realised the challenges faced in explaining our project. Both the theoretical concepts and the practical output of the project were elaborate. It takes time to explain the mathematical background, the intermediate stages of appropriating foreign theories and concepts, to exemplify these processes and, at the end of the day, to discuss the output.
In 2019, the city of Graz initiated the cultural year Kulturjahr 2020 Graz.1https://www.kulturjahr2020.at Under the premise Wie wir leben wollen (How we want to live), a call was publicised for projects to address questions of contemporary society. The authors of this article submitted (and were granted) a proposal for a pop-up exhibition space, that is, a shop-front meeting place for people to drop in and be guided through our Mathematics & Arts projects. We named this exhibition project Listen2Intuition.
2.1 How to address a wider audience?
With neither mathematics nor contemporary music being a natural favourite for a wider audience, one of our challenges was to attract visitors in the first place.
In the planning of Listen2Intuition as a pop-up exhibition space, we were hoping for a good amount of curious people just dropping in by chance. However, even with a popular lunch place located next door, only a few people would just happen to walk in. Not for lack of interest per se. Rather, it seems that everybody has such a busy schedule that before walking into an exhibition by chance, you are already walking somewhere else.
More effective in publicising the exhibition were a well-set-up website2https://www.listentointuition.com and social media activities. What seemed to work best was old fashion invitations and the word of mouth, that Listen2Intuition is something one should visit.
The following two subsections, 2.2 and 2.3, provide some mathematical background relevant to our project.
2.2 Cluster combinatorics and algebraic structures of triangulations
In algebra, a quiver is an oriented graph, possibly with loops and multiple edges between vertices. A quiver encodes interactions between mathematical objects (its vertices), while arrows describe the direction of the interactions.
Quivers and their mutations have become very popular in algebra, as they play a key role in the theory of cluster combinatorics, developed first by Fomin and Zelevinsky in, e.g., [6 S. Fomin and A. Zelevinsky, Cluster algebras. I. Foundations. J. Amer. Math. Soc. 15, 497–529 (2002) , 7 S. Fomin and A. Zelevinsky, Cluster algebras. II. Finite type classification. Invent. Math. 154, 63–121 (2003) ], and on the categorical side, by Buan et al., [3 A. B. Buan, B. R. Marsh, M. Reineke, I. Reiten and G. Todorov, Tilting theory and cluster combinatorics. Adv. Math. 204, 572–618 (2006) ] and by Caldero et al. [4 P. Caldero, F. Chapoton and R. Schiffler, Quivers with relations arising from clusters (An case). Trans. Amer. Math. Soc. 358, 1347–1364 (2006) ]; see [1 K. Baur, Polygone, Clusteralgebren und Clusterkategorien. In Facettenreiche Mathematik, pp. 43–66, Vieweg+Teubner Verlag, Wiesbaden (2011) ] for an overview.
A key source for quivers in this context – quivers without loops and 2-cycles – are triangulations of surfaces. Among them, annuli are of particular interest: The associated quivers are manageable, yet the triangulations provide infinite-type cluster structures which exhibit interesting dynamics.
2.3 Collective behaviour and swarming patterns
Swarming patterns form due to the collective behaviour of a large number of individuals. Despite all individuals being subject to the same interaction law, collective behaviour, and swarming in particular, can feature highly complicated dynamics due to the amount of crisscross interactions.
Numerical simulation of a swarm of particles.
🅭🅯 CC BY 4.0Many models of collective behaviour share a common mathematical description in terms of gradient-flow differential equations or discrete stochastic models. Figure 3 shows an example of a large swarm of particles spreading over a sphere. Repulsive–attractive interactions describe individuals that retract when being too close to one another, yet come closer together when being too far away from one another. Examples are provided by the Lennard-Jones potential describing, e.g., crystallisation, or the Morse potential modelling biological swarms. Repulsive–attractive interaction potentials give rise to a stunningly rich variety of patterns, which depend on the details of the interaction potentials in a highly complex (yet not chaotic) manner, see, e.g., [5 K. Fellner and G. Raoul, Stable stationary states of non-local interaction equations. Math. Models Methods Appl. Sci. 20, 2267–2291 (2010) , 8 E. J. Hackett-Jones, K. A. Landman and K. Fellner, Aggregation patterns from nonlocal interactions: Discrete stochastic and continuum modeling. Phys. Rev. E 85, article no. 041912 (2012) , 9 J. H. von Brecht, D. Uminsky, T. Kolokolnikov and A. L. Bertozzi, Predicting pattern formation in particle interactions. Math. Models Methods Appl. Sci. 22, article no. 1140002 (2012) ].
2.4 Growth behaviour of infinite friezes
The interdisciplinary cooperation within our team was not exclusively directed towards connecting mathematics and arts on an eye-to-eye level. In fact, as it happened, we found also connections between the algebra of frieze patterns, in particular properties of so-called growth coefficients of infinite friezes, and ideas from dynamical systems; these were published in [2 K. Baur, K. Fellner, M. J. Parsons and M. Tschabold, Growth behaviour of periodic tame friezes. Rev. Mat. Iberoam. 35, 575–606 (2019) ].
3 Listen2Intuition: An interactive exhibition in four stages
Our exhibition concept for Listen2Intuition divided the experience into four main stages (stations).
Do-it-yourself triangulation.
🅭🅯 CC BY 4.0The first stage started by presenting the topological triangulations of Figure 1. The visitors were right away invited to invent their own “triangulation” by using a thread that loops around pins as corner points, see Figure 4. We insisted that visitors should feel free to do what they felt like doing as triangulations, and that nothing would be regarded as a mistake. The intention was to be as interactive as possible and to remove any previous-knowledge bias. Even the four-year-old daughter of Fellner and Friebel had great fun making her own triangulations on the pin board.
Next, visitors were presented graphical works, see Figure 5, which were part of the appropriation process of Tamara Friebel leading to the composition Attractive Privacies of Breathing Borders for five singers and flute. For example, Figure 2 shows on the top left the triangulation which served as a basic concept of the musicians (five singers and one flute) and how they would relate to one another according to the edges connecting corner points. On the top right, the colourful sketch shows a much more advanced graphical appropriation, which intuitively represents qualities of the later composition Attractive Privacies, the final score of which is shown at the bottom of Figure 2.
Discover your attractive privacies.
🅭🅯 CC BY 4.0An important part of the first exhibition stage was also the following anecdote: On one occasion, Tamara Friebel invited professional musicians to improvise the colourful sketch plotted on the top right in Figure 2 as a graphical score. They would only use the syllable OM and not yet know the final score. The musicians were also told the basic concept that the edges of the triangulation represent which musicians could directly communicate with one another and which not. Also, that the flute as the central instrument would have the capacity of linking everybody.
Given only these concepts and the colourful sketch in Figure 2 to be interpreted as a graphical score, the six musicians came up with an improvisation, which sounded relatively similar to the final composition Attractive Privacies (of course, without being as refined as a crafted piece). As astounding as this anecdote might sound, it becomes more tangible if one recalls that musicians will always listen to one another even when improvising. They will intuitively form a collective and, when guided by the right input, intuitively appropriate the given material, not unlike how this was done by Friebel in the composition process.
Take-away message The following observation was a highly interesting aspect of the first stage: We had a total of about 150 guests each making a do-it-yourself triangulation, but no two resembled each other. The combinatorial possibilities are just too many to see repetitions within a sample of 150 tries. The artistic appropriation, however, which is the colourful sketch in Figure 2 together with the rules of interrelating voices, was successful in distilling an essence of the final composition Attractive Privacies of Breathing Borders. At least in the sense that with improvisation and composition being similar, one could say that the task became intuitively understandable and essentially reproducible within the paradigm of a musical performance.
The second stage of the exhibition can be seen in Figure 6. It is fair to say that this stage was the one closest related to the name Listen2Intuition.
Listen and see.
🅭🅯 CC BY 4.0In an intimate corner with high-quality loudspeakers, a loop of a 1 min 15 sec excerpt of the composition The Agility was playing, a duo for violin and guitar written for and first performed at Wien Modern.3Excerpt of Tamara Friebel’s The Agility of Perspective Nearness in a lake of being, performed by Duo Hedda: https://vimeo.com/482416548 from 41:15 until 42:30. Visitors would experience 40 sec of pure sound with black screen and 35 sec of sound with the video from the live performance. The score of the excerpt could be read along the wall.
The composition The Agility brought together the two aforementioned instruments, violin and guitar, whose sounds (despite both being string instruments) do not really mix (which was actually a reason for the composition to be originally commissioned). Visitors were given 3D prints of geometric forms, which were derived from the formal studies on triangulations. Amongst the many formal studies, there was one featuring two subunits, which would not really fit together, yet superpose to a larger entity. These 3D prints were handed to the audience as a metaphor of how a composition was supposed to bring together sounds that do not mix. The audience was then invited to listen to the music. They were asked to use their individual intuition to experience this music, which is actually better than words, to be able to express how two units can be part of an entity while remaining distinct.
By this time in the exhibition experience, the great majority of visitors realised that Listen2Intuition succeeded to draw their mindset into accessing new worlds – worlds that are not imposed by the exhibition’s team, but which open up according to the individual personality of the visitors.
Take-away message The exhibition team felt very positive that Listen2Intuition succeeded to fascinate all (minus one) visitors despite (or rather because of) the quite challenging content, and regardless of any previous knowledge.
The third stage invited visitors to another interactive activity. Figure 7 shows a visitor, who played a zither using ping pong balls. The sound would be recorded using a pick-up microphone, transferred to a laptop, and processed in real time by the music software Max/MSP. A so-called Max patch modulated the sound based on the collective behaviour of a simulated swarm and then played it back to the visitor over the loudspeaker in the middle of the table.
Experience your collective awareness.
🅭🅯 CC BY 4.0The visitors were given the task to improvise whatever came to mind while observing a “video-score” on the computer screen (again under the premise that they should feel free to do what felt right and nothing was regarded as a mistake).
As part of the third stage, the exhibition team would tell the visitors that by tuning up and down the volume of the loudspeaker with the feedback sound, they would be able to explore the richness of the sounds produced using the rich collective behaviour of a swarm dynamics. From a mathematical point of view, it should be added that there are somehow too many swarming models exhibiting what a human would always intuitively classify as swarming behaviour. In contrast to other areas of applied mathematics, where prototypical equations, like the heat equation, form the basis of a great many of related mathematical models, there exists no single prototypical swarming model.
Take-away message Stage three of our exhibition wanted to bypass any mechanistic explanation of swarming patterns and collective behaviour. We rather wanted to provide an intuitive experience and allow visitors to develop a kind of self-understanding of collective dynamics based on a sound feedback.
The fourth stage invited the visitors into a curtained-off space. There, the composition Dance Me to My Rebirth4Excerpt of Tamara Friebel’s Dance Me to My Rebirth, performed by Maja Mijatović: https://www.youtube.com/watch?v=MWDFL1bJ6XU. for harpsichord and electronics by Tamara Friebel was played along a video showing swarming patterns. In fact, Figure 3 is a still from that video. Visitors were informed that the task of stage three was also given to the performer Maja Mijatović (yet using the string of the harpsichord instead of a zither, which was the exhibition’s practical alternative to a delicate harpsichord). Maja’s improvisation was recorded and then used as a layer of electronic music juxtaposed on top of the harpsichord performance of the score of Dance Me to My Rebirth.
Hearing the final composition Dance Me to My Rebirth for harpsichord and electronics allowed the visitors to relate to their own improvisation experience at stage three. Moreover, being in a darkened space exposed only to video and music gave the opportunity to further process the exhibition experience.
Overall, Listen2Intuition was a great experience for the exhibition team/authors as well as for the visitors. The feedback was so positive that we reopened the exhibition for an additional two weeks later in the year. In total we had about 150 visitors with an age range from 4 to 84 years. On average, every visitor spent almost an hour in the exhibition, which reflects the intensity of the engagement we were so happy to witness. Some visitors did even come back and donate contributions or little artworks to a public board of responses.
3.1 Listen2Intuition will come to Paris in 2024
Listen2Intuition will welcome visitors at the Maison Poincaré in Paris5https://maison-des-maths.paris from April to July 2024. Please check the website of the Maison Poincaré for the details to be specified.
Acknowledgements. The authors were supported by the project Mathematics & Arts: Towards a balance between artistic intuition and mathematical complexity funded by the University of Graz.
- 1
- 2
- 3
Excerpt of Tamara Friebel’s The Agility of Perspective Nearness in a lake of being, performed by Duo Hedda: https://vimeo.com/482416548 from 41:15 until 42:30.
- 4
Excerpt of Tamara Friebel’s Dance Me to My Rebirth, performed by Maja Mijatović: https://www.youtube.com/watch?v=MWDFL1bJ6XU.
- 5
References
- K. Baur, Polygone, Clusteralgebren und Clusterkategorien. In Facettenreiche Mathematik, pp. 43–66, Vieweg+Teubner Verlag, Wiesbaden (2011)
- K. Baur, K. Fellner, M. J. Parsons and M. Tschabold, Growth behaviour of periodic tame friezes. Rev. Mat. Iberoam. 35, 575–606 (2019)
- A. B. Buan, B. R. Marsh, M. Reineke, I. Reiten and G. Todorov, Tilting theory and cluster combinatorics. Adv. Math. 204, 572–618 (2006)
- P. Caldero, F. Chapoton and R. Schiffler, Quivers with relations arising from clusters (An case). Trans. Amer. Math. Soc. 358, 1347–1364 (2006)
- K. Fellner and G. Raoul, Stable stationary states of non-local interaction equations. Math. Models Methods Appl. Sci. 20, 2267–2291 (2010)
- S. Fomin and A. Zelevinsky, Cluster algebras. I. Foundations. J. Amer. Math. Soc. 15, 497–529 (2002)
- S. Fomin and A. Zelevinsky, Cluster algebras. II. Finite type classification. Invent. Math. 154, 63–121 (2003)
- E. J. Hackett-Jones, K. A. Landman and K. Fellner, Aggregation patterns from nonlocal interactions: Discrete stochastic and continuum modeling. Phys. Rev. E 85, article no. 041912 (2012)
- J. H. von Brecht, D. Uminsky, T. Kolokolnikov and A. L. Bertozzi, Predicting pattern formation in particle interactions. Math. Models Methods Appl. Sci. 22, article no. 1140002 (2012)
- I. Xenakis, Formalized music: Thought and mathematics in composition, Pendragon Press, NY (2001)
Cite this article
Karin Baur, Klemens Fellner, Tamara Friebel, Listen2Intuition: A Mathematics & Arts exhibition project. Eur. Math. Soc. Mag. 129 (2023), pp. 13–19
DOI 10.4171/MAG/149